Advertisements (Quảng cáo)
Cho đường tròn \((C)\) có tâm \(O\) bán kính \(R\) và đường thẳng \(\Delta \) không cắt \((C)\). Chứng minh rằng tập hợp tâm các đường tròn tiếp xúc với \(\Delta \) và tiếp xúc ngoài với \((C)\) nằm trên một parabol. Tìm tiêu điểm và đường chuẩn của parabol đó.
(h.119).
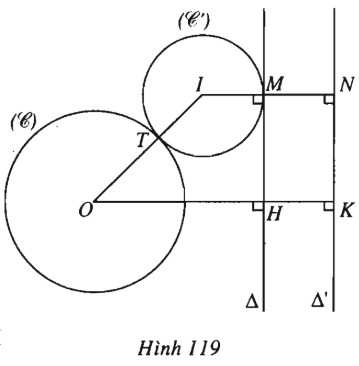
Kẻ \(OH\) vuông góc với \(\Delta \) và kéo dài \(OH\) (về phía \(H\)) một đoạn \(HK=R.\)
Dựng đường thẳng \(\Delta ‘\) đi qua \(K\) và song song với \(\Delta \). Khi đó \(\Delta ‘\) cố định và không đi qua \(O\).
Advertisements (Quảng cáo)
Xét đường tròn \((C’)\) tâm \(I\) tiếp xúc ngoài với \((C)\) tại \(T\) và tiếp xúc với \(\Delta \) tại \(M\). Gọi \(N\) là giao điểm của đường thẳng \(IM\) và \(\Delta ‘\).
Ta có: \(IO = OT + TI \)
\(= R + IM = IN = d(I;\Delta ‘)\).
Vậy \(I\) nằm trên paprbol nhận \(O\) làm tiêu điểm và \(\Delta ‘\) làm đường chuẩn.