Câu 12 trang 240 SBT Đại số 10 Nâng cao. + Có hai điểm chung phân biệt khi \(m < 6;\). BÀI TẬP ÔN TẬP CUỐI NĂM - ĐẠI SỐ 10 NÂNG CAO
Dùng đồ thị để biện luận số nghiệm của phương trình:
\({x^2} - 6x + 3 + m = 0.\)
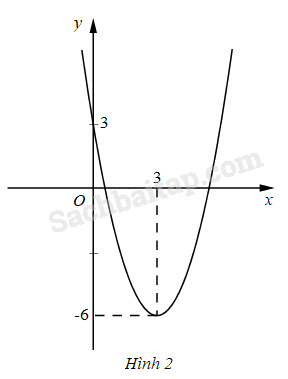
Xét hàm số \(y = f\left( x \right) = {x^2} - 6x + 3.\) Đồ thị hàm số là một parabol quay bề lõm lên trên (h.2) và đỉnh parabol là điểm \(P\left( {3; - 6} \right)\).
Do đó parabol có phương trình \(y = {x^2} - 6x + 3\) và đường thẳng có phương trình \(y = - m:\)
+ Có một điểm chung duy nhất khi \(m = 6;\)
Advertisements (Quảng cáo)
+ Có hai điểm chung phân biệt khi \(m < 6;\)
+ Không có điểm chung khi \(m > 6.\)
Suy ra phương trình \({x^2} - 6x + 3 + m = 0\)
+ Có nghiệm kép khi \(m = 6;\)
+Có hai nghiệm phân biệt khi \(m < 6;\)
+ Vô nghiệm khi \(m > 6.\)