Cho hàm số \(y = - {x^2} + 4x - 3\)
a. Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho.
b. Dựa vào đồ thị, hãy nêu các khoảng trên đó hàm số chỉ nhận giá trị dương.
c. Dựa vào đồ thị, hãy nêu các khoảng trên đó hàm số chỉ nhận giá trị âm.

a. Hàm số \(y = - {x^2} + 4x - 3\) có thể viết được dưới dạng
\(y = - {\left( {x - 2} \right)^2} + 1\)
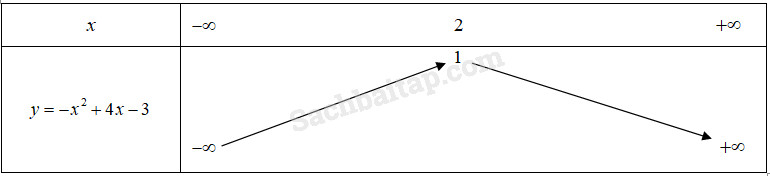
Từ đó suy ra hàm số đồng biến trên khoảng \(\left( { - \infty ;2} \right),\) nghịch biến trên khoảng \(\left( {2; + \infty } \right).\)
Bảng biến thiên :
Advertisements (Quảng cáo)
Hàm số có giá trị lớn nhất bằng 1 khi \(x = 2.\)
Đồ thị của nó là một parabol đi qua các điểm
\((0 ; -3), (1 ; 0),\) \( (2 ; 1), (3 ; 0), (4 ; -3)\)
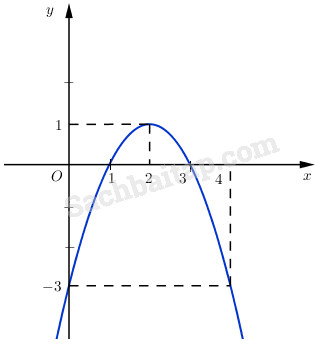
Từ đồ thị ta thấy :
b. Hàm số chỉ nhận giá trị dương nếu \(x \in (1 ; 3).\)
c. Hàm số chỉ nhận giá trị âm nếu
\(x \in \left( { - \infty ;1} \right) \cup \left( {3; + \infty } \right)\)
