Sử dụng đồ thị để biện luận số nghiệm của các phương trình sau theo tham số k :
a. \(3{x^2} - 2x = k\)
b. \({x^2} - 3\left| x \right| - k + 1 = 0\)

a. Vẽ parabol \(y = 3x^2 - 2x\) và xét đường thẳng \(y = k\) (h. 3.3), ta có :
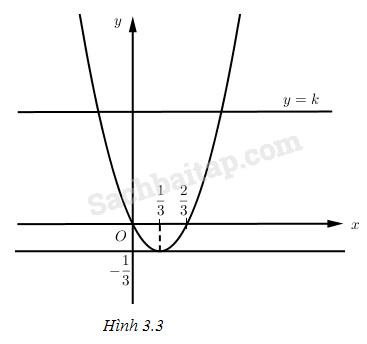
• Nếu \(k < - \dfrac{1}{3}\) thì phương trình vô nghiệm.
• Nếu \(k = - \dfrac{1}{3}\) thì phương trình có một nghiệm (kép)
• Nếu \(k > - \dfrac{1}{3}\) thì phương trình có hai nghiệm phân biệt.
Chú ý. Kết quả trên cũng có thể được kiểm nghiệm lại bằng phương trình bậc hai \(3x^2 - 2x - k = 0,\) với biệt thức thu gọn là \(\Delta ‘ = 1 + 3k.\)
Advertisements (Quảng cáo)
b. Vẽ đồ thị của hàm số \(y = {x^2} - 3\left| x \right| + 1\) và đường thẳng \(y = k\) (h. 3.4), ta có :
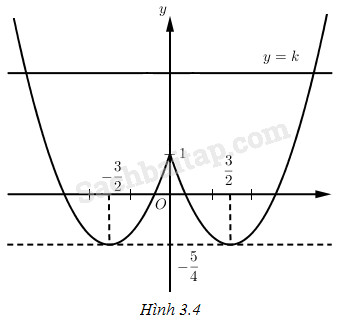
• Nếu \(k < - \dfrac{5}{4}\) thì phương trình vô nghiệm.
• Nếu \(k = - \dfrac{5}{4}\) thì phương trình có hai nghiệm (cả hai đều là nghiệm kép).
• Nếu \( - \dfrac{5}{4} < k < 1\) thì phương trình có 4 nghiệm.
• Nếu k = 1 thì phương trình có 3 nghiệm.
• Nếu k ≥ 1 thì phương trình có 2 nghiệm.
Chú ý. Có thể kiệm nghiệm lại kết quả trên bằng cách giải và biện luận phương trình đã cho theo tham số k.
