Cho một tấm tôn hình chữ nhật có kích thước 80 cm x 50 cm. Hãy cắt đi ở bốn góc vuông những hình vuông bằng nhau để khi gập lại theo mép cắt thì được một cái hộp (không nắp) có thể tích lớn nhất.
 :
:
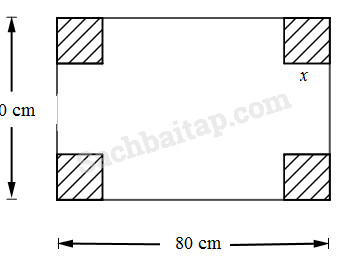
Gọi cạnh hình vuông được cắt là \(9x\) (\(0 < x < 25\), đơn vị : xentimét)
Thể tích V của cái hộp là
\(V = x\left( {80 - 2{x}} \right)\left( {50 - 2{x}} \right)\)
Khi đó ta có
\(\begin{array}{l}12V = 6{x}\left( {80 - 2{x}} \right)\left( {100 - 4{x}} \right)\\ \le {\left( {\dfrac{{6{x} + 80 - 2{x} + 100 - 4{x}}}{3}} \right)^3} = {60^{3.}}\end{array}\)
Advertisements (Quảng cáo)
Suy ra \(V \le \dfrac{{{{60}^3}}}{{12}}\) hay \(V \le 18\,000\)
Đẳng thức xảy ra khi và chỉ khi \(6x = 80 – 2x = 100 – 4x\) tức là \(x = 10.\)
Giá trị lớn nhất của V là 18000 cm3 khi \(x = 10 (cm)\)
Vậy phải cắt đi ở bốn góc vuông của hình chữ nhật ban đầu những hình vuông có cạnh 10 cm.
Nhận xét. Nếu xét \(4V = 4{x}\left( {80 - 2{x}} \right)\left( {50 - 2{x}} \right)\) thì 4V là tích của ba thừa số có tổng không đổi (bằng 130), ta vẫn có bất đẳng thức \(4V \le {\left( {\dfrac{{130}}{3}} \right)^3}\) nhưng đẳng thức không thể xảy ra và không có giá trị nào của x thỏa mãn
\(80 - 2{x} = 50 - 2{x}\)
