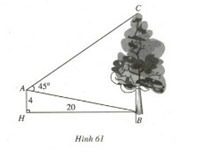
Bài 37. Từ vị trí \(A\) người ta quan sát một cây cao (h.61)
Biết \(AH = 4\,m,\,HB = 20\,m,\,\widehat {BAC} = {45^0}\). Tính chiều cao của cây.

Tam giác \(AHB\) vuông tại \(H\) nên \(A{B^2} = A{H^2} + H{B^2} = {4^2} + {20^2} = 416\)
\(\eqalign{
& \Rightarrow AB \approx 20,4 \cr
& \tan \widehat {BAH} = {{HB} \over {HA}} = {{20} \over 4} = 5 \cr
& \Rightarrow \,\,\,\,\widehat {BAH} \approx 78,{7^0} \cr
& \Rightarrow \,\,\,\,\widehat {HAC} \approx 78,{7^0} + {45^0} \approx 123,{7^0} \cr}\)
Advertisements (Quảng cáo)
\(\eqalign{
& \widehat {HAB} + \widehat {HBA} = {90^0} \cr
& \widehat {ABC} + \widehat {HBA} = {90^0} \cr
& \Rightarrow \widehat {HAB} = \widehat {ABC} \cr
& \Rightarrow \widehat {BCA} = {180^0} - \widehat {BAC} - \widehat {ABC} = {180^0} - \widehat {HAC} \cr} \)
\(\Rightarrow \,\,\,\,\widehat {BCA} \approx {180^0} - 123,{7^0} = 56,{3^0}.\)
Ta có \({{BC} \over {{\mathop{\rm s}\nolimits} {\rm{in4}}{5^0}}} = {{AB} \over {{\mathop{\rm s}\nolimits} {\rm{in56,}}{{\rm{3}}^0}}}\)
\(\Rightarrow \,\,BC = {{20,4} \over {{\mathop{\rm s}\nolimits} {\rm{in56,}}{{\rm{3}}^0}}}{\mathop{\rm s}\nolimits} {\rm{in4}}{5^0} \approx 17,4\)
Vậy cây cao \(17,4\) m.
