Giả sử (G) là đồ thị của hàm số y = f(x) xác định trên tập D và A là một điểm trên trục hoành có hoành độ bằng a. Từ A, ta dựng đường thẳng (d) song song (hoặc trùng) với trục tung.
a) Khi nào thì (d) có điểm chung với (G)? (Hướng dẫn: Xét hai trường hợp a thuộc D và a không thuộc D)
b) (d) có thể có bao nhiêu điểm chung với (G)? Vì sao?
c) Đường tròn có thể là đồ thị của hàm số nào không? Vì sao?

Advertisements (Quảng cáo)
a) Khi a ∈ D thì d có điểm chung với (G) và khi a ∉ D thì (d) không có điểm chung với (G).
b) (d) có nhiều nhất một điểm chung với (G) vì nếu a ∈ D thì có duy nhất một giá trị f(a), lúc đó (d) cắt (G) tại điểm duy nhất với M(a, f(a))
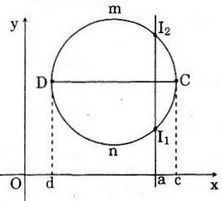
c) Đường tròn không thể là đồ thị của một hàm số vì đường thẳng song song với Oy cắt đường tròn tại hai điểm phân biệt.