Bài 2 trang 45 sgk hình học 10: Bài 2. Tích vô hướng của hai vectơ. 2. Cho ba điểm O, A, B thẳng hàng biết OA = a, OB = b
Bài 2. Cho ba điểm \(O, A, B\) thẳng hàng biết \(OA = a, OB = b\). tính tích vô hướng của \(\vec{OA}\).\(\vec{OB}\) trong \(2\) trường hợp
a) Điểm \(O\) nằm ngoài đoạn \(AB\)
b) Điểm \(O\) nằm trong đoạn \(AB\)
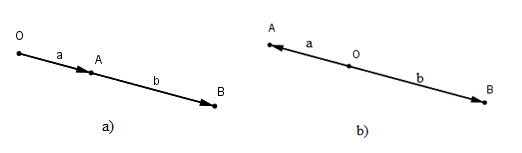
a) Khi \(O\) nằm ngoài đoạn \(AB\) thì hai vec tơ \(\vec{OA}\) và \(\vec{OB}\) cùng hướng và góc
Advertisements (Quảng cáo)
\((\vec{OA}, \vec{OB}) = 0^0\)
\(\cos(\vec{OA}, \vec{OB}) = 1\) nên \(\vec{OA}.\vec{OB} = a.b\)
b) Khi \(O\) nằm ngoài trong đoạn \(AB\) thì hai vectơ \(\vec{OA}\) và \(\vec{OB}\) ngược hướng và góc
(\(\vec{OA}, \vec{OB}) = 180^0\)
\(\cos(\vec{OA}, \vec{OB}) = -1\) nên \(\vec{OA}.\vec{OB} = -a.b\)