Advertisements (Quảng cáo)
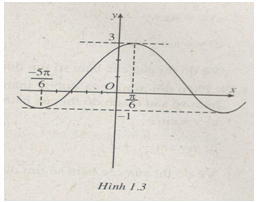
Cho biết đồ thị (h.1.3) sau là đồ thị hàm số \(y = A\sin \left( {x + \alpha } \right) + B\) (\(A,B,\alpha \) là những hằng số). Hãy xác định \(A,B,\alpha \).
Giải
Hàm số \(y = A\sin \left( {x + \alpha } \right) + B\) đạt giá trị lớn nhất là 3 tại \(x = {\pi \over 6}\) (coi \(A > 0\)) nên:
\(\left\{ \matrix{
\sin \left( {{\pi \over 6} + \alpha } \right) = 1 \hfill \cr
A + B = 3 \hfill \cr} \right.\)
Hàm số \(y = A\sin \left( {x + \alpha } \right) + B\) đạt giá trị nhỏ nhất là -1 tại \(x = – {{5\pi } \over 6}\) nên:
\(\left\{ \matrix{
\sin \left( { – {{5\pi } \over 6} + \alpha } \right) = – 1 \hfill \cr
– A + B = – 1 \hfill \cr} \right.\)
Advertisements (Quảng cáo)
Từ đó \(B = 1,A = 2\) và chú ý rằng
\(\sin \left( { – {{5\pi } \over 6} + \alpha } \right) = \sin \left( {{\pi \over 6} + \alpha – \pi } \right) = \sin \left( {{\pi \over 6} + \alpha } \right)\)
Nên chỉ cần chọn \(\alpha \) sao cho \(\left( {{\pi \over 6} + \alpha } \right) = 1,\) chẳng hạn \(\alpha = {\pi \over 3}\)
Vậy \(A = 2,B = 1,\alpha = {\pi \over 3}\)