Một cách trình bày việc đưa biểu thức \(a\sin x + b\cos x\) (a, b là hằng số, \({a^2} + {b^2} \ne 0\)) về dạng \(C\sin \left( {x + \alpha } \right)\) nhờ biểu thức toạn độ của tích vô hướng của hai vectơ
Trong mặt phẳng tọa độ gắn với đường tròn lượng giác tâm O gốc A, hãy xét các điểm \(P\left( {a;b} \right),Q\left( {b;a} \right),M\left( {\cos x;\sin x} \right)\)
a) Từ công thức \(\overrightarrow {OQ} .\overrightarrow {OM} = a\sin x + b\cos x\) và
\(\overrightarrow {OQ} .\overrightarrow {OM} = \left| {\overrightarrow {OQ} } \right|.\left| {\overrightarrow {OM} } \right|\cos \left( {OQ,QM} \right)\)
Hãy suy ra \(a\sin x + b\cos x = C\cos \left( {x - \beta } \right)\) trong đó \(\beta \) là số đo của góc lượng giác \(\left( {OA,OQ} \right)\)
b) Từ câu a) suy ra rằng \(a\sin x + b\cos x = C\sin \left( {x + \alpha } \right)\) trong đó \(\alpha \) là số đo của góc lượng giác \(\left( {OA,OP} \right),C = \left| {\overrightarrow {OP} } \right|\)
Giải
a) Ta có \(\overrightarrow {OQ} .\overrightarrow {OM} = a\sin x + b\cos x\)
\(\eqalign{
& = \left| {\overrightarrow {OQ} } \right|.\left| {\overrightarrow {OM} } \right|\cos \left( {OQ,OM} \right) \cr&= \left| {\overrightarrow {OQ} } \right|\cos (\left( {OA,OM} \right) - \left( {OA,OQ} \right)) \cr
& = \left| {\overrightarrow {OQ} } \right|\cos \left( {\alpha - \beta } \right),\cr&\left| {\overrightarrow {OQ} } \right| = \sqrt {{a^2} + {b^2}} ,\beta = \left( {OA,OQ} \right) \cr} \)
Advertisements (Quảng cáo)
b)
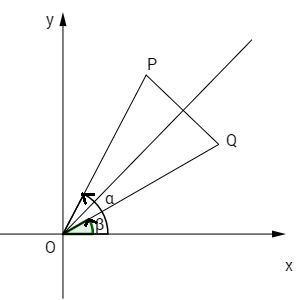
Hai điểm \(P\left( {a;b} \right)\) và \(Q\left( {b;a} \right)\) đối xứng qua đường phân giác của góc phần tư thứ nhất của hệ tọa độ, nên dễ thấy
\(\left( {OA,OQ} \right) = {\pi \over 2} - \left( {OA,OP} \right),\) tức là
\(\beta = {\pi \over 2} - \alpha + k2\pi ,k \in Z.\)
Vậy
\(a\sin x + b\cos x = \left| {\overrightarrow {OQ} } \right|\cos x\left( {x - \beta } \right)\)
\(= \left| {\overrightarrow {OP} } \right|\cos \left( {x - {\pi \over 2} + \alpha } \right) = \left| {\overrightarrow {OP} } \right|\sin \left( {x + \alpha } \right)\)
sachaitap.com
