15. Trang 52 Sách bài tập Hình học 11 nâng cao.
Cho hình chóp S.ABCD có đáy là hình thang \(\left( {AB//CD,AB > CD} \right).\) Gọi I, J theo thứ tự là trung điểm của các cạnh SB và SC.
a) Xác định giao tuyến của hai mặt phẳng (SAD) và (SBC).
b) Tìm giao điểm của đường thẳng SD với mp(AIJ).
c) Xác định thiết diện của hình chóp S.ABCD cắt bởi mp(AIJ).

Advertisements (Quảng cáo)
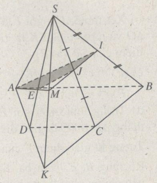
a) Gọi K là giao điểm của AD và BC, khi đó hai mặt phẳng (SAD) và (SBC) có hai điểm chung S và K. Vậy giao tuyến của chúng là đường thẳng SK.
b) Gọi M là giao điểm của IJ và SK. Khi đó: \(\left( {SAD} \right) \cap \left( {AIJ} \right) = AM.\)
Gọi E là giao điểm của AM và SD thì E chính là giao điểm của SD với mp(AIJ).
c) Thiết diện của hình chóp khi cắt bởi mp(AIJ) là tứ giác AIJE.
