Cho tam giác ABC vuông ở A, AB = c,AC = b. Trên đường thẳng d vuông góc với mp(ABC) tại A, lấy điểm S bất kì, \(S \ne A\) . Gọi B1, C1 lần lượt là hình chiếu của A trên SB, SC.
1. Xác định tâm của mặt cầu đi qua các điểm A, B, C, B1, C1 và tính bán kính của mặt cầu đó.
2.Cho SA = h, tính tỉ số thể tích của hai tứ diện SA B1C1 và SABC.

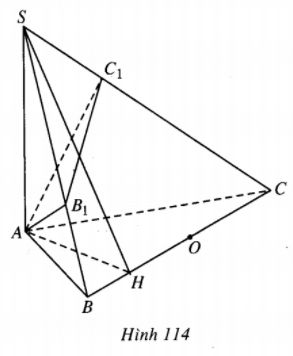
1.Ta có AC \( \bot \) mp(SAB) nến AC\( \bot \)SB, từ đó SB \( \bot \) B1C tức là \(\widehat {B{B_1}C} = {90^0}\)
Tương tự ta cũng có \(\widehat {B{C_1}C} = {90^0}\). Vậy tâm mặt cầu đi qua B, C, A, B1, C1 là trung điểm O của BC.
Advertisements (Quảng cáo)
Ta có \(AO = {1 \over 2}{\rm{ }}BC,\)
\(B{C^2} = A{B^2} + A{C^2} = {\rm{ }}{b^2} + {\rm{ }}{c^2}.\)
Từ đó bán kính mặt cầu bằng\({{\sqrt {{b^2} + {\rm{ }}{c^2}} } \over 2}.\)
2. Ta có
\({{{V_{S.A{B_1}{C_1}}}} \over {{V_{S.ABC}}}} = {{SA} \over {SA}}.{{S{B_1}} \over {SB}}.{{S{C_1}} \over {SC}} \)
\(= {{S{B_1}.SB} \over {S{B^2}}}.{{S{C_1}.SC} \over {S{C^2}}} = {{S{A^2}} \over {S{B^2}}}.{{S{A^2}} \over {S{C^2}}} = {{{h^4}} \over {\left( {{h^2} + {c^2}} \right)\left( {{h^2} + {b^2}} \right)}}.\)
Vậy tỉ số thể tích của hai tứ diện \(SA{B_1}{C_1}\) và \(SABC\) bằng \({{{h^4}} \over {({h^2} + {b^2})({h^2} + {c^2})}}.\)
