Cho hình chóp S.ABC. Biết rằng các điểm A, B, C và các trung điểm A‘, B‘, C‘ của các cạnh SA, SB, SC cùng thuộc một mặt cầu bán kính R.
1. Chứng minh rằng tâm mặt cầu ngoại tiếp hình chóp S.ABC thuộc đường cao SH của hình chóp.
2. Cho góc giữa đường thẳng SC và mặt phẳng (ABC) bằng 60°, chứng minh rằng H là tâm của mặt cầu đi qua sáu điểm A, B,C, A’ ,B’ ,C’.
Khi đó, hãy tính diện tích mặt cầu ngoại tiếp hình chóp S.ABC.

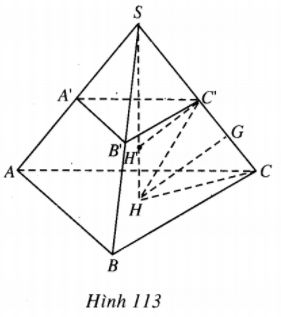
1. Vì A, B, A‘, B‘ cùng thuộc một mặt cầu và A‘B‘//AB nên ABBA‘ là hình thang cân, từ đó SA = SB. Lập luận tương tự ta có SB = SC.
Vậy SA = SB = SC.
Advertisements (Quảng cáo)
Suy ra đường cao SH của hình chóp S.ABC chính là trục của tam giác ABC. Do đó, tâm của mặt cầu ngoại tiếp hình chóp S.ABC thuộc SH.
2. Ta sẽ chứng minh H chính là tâm của mặt cầu đi qua các điểm A, B, C, A‘, B‘, C‘, Thật vậy, do SH \( \bot \) mp(ABC) nên từ đó \(HC{\rm{ }} = {1 \over 2}SC,\) mặt khác C‘S = C‘C nên\(HC’ = {1 \over 2}SC\).
Từ chứng minh trên ta có HA = HB = HC = HC‘ = HA‘ = HB’, tức H là tâm của mặt cầu đi qua A, B, C, A‘, B‘, C‘.
Gọi G là trung điểm của C‘C thì HG \( \bot \) SC. Kẻ C‘H‘ song song với GH \(\left( {H’ \in SH} \right)\) thì H‘S = H‘C, từ đó H‘ là tâm mặt cầu ngoại tiếp hình chóp S.ABC và H‘S là bán kính mặt cầu ngoại tiếp S.ABC.
Ta có \(H'{S^2} = H’C{‘^2} + SC'{^2}\) ,mặt khác
\(H’C’ = {2 \over 3}HG,HG = {{R\sqrt 3 } \over 2},SC’ = {{SC} \over 2} = R.\)
Từ đó \(H'{S^2} = {\left( {{2 \over 3}.{{R\sqrt 3 } \over 2}} \right)^2} + {R^2} = {{{R^2}} \over 3} + {R^2} = {{4{R^2}} \over 3}.\)
Vậy diện tích mặt cầu ngoại tiếp hình chóp S.ABC là \({{16\pi {R^2}} \over 3}.\)
