Cho tam giác cân ABC, AB = AC. Một điểm M thay đổi trên đường thẳng vuông góc với mặt phẳng (ABC) tại A (M không trùng với điểm A).
a) Tìm quỹ tích trọng tâm G và trực tâm H của tam giác MBC.
b) Gọi O là trực tâm của tam giác ABC, hãy xác định vị trí của điểm M để thể tích khối tứ diện OHBC đạt giá trị lớn nhất.

a)
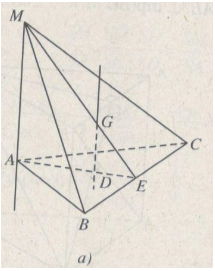
Nếu gọi E là trung điểm của BC (h.l08a) thì trọng tâm G của tam giác MBC xác định bởi \(\overrightarrow {EG} = {1 \over 3}\overrightarrow {EM} .\) Từ đó, khi M vạch đường thẳng \(\Delta \) vuông góc với mp(ABC) tại A \(\left( {M \ne \;A} \right)\) thì G vạch đường thẳng \(\Delta \)’ vuông góc với mp(ABC) tại trọng tâm D của tam giác ABC (trừ điểm D).
Do AB = AC nên các tam giác vuông MAB, MAC bằng nhau, vậy ME và AE cùng vuông góc với BC. Từ đó trực tâm H của tam giác MBC thuộc ME (h.l08b)
Trong mặt phẳng (AME), đường thẳng vuông góc với ME tại trực tâm H của tam giác MBC cắt AE tại O thì do BC \( \bot \) (AEM) nên BC \( \bot \) OH, từ đó OH \( \bot \) (MBC).
Advertisements (Quảng cáo)
Ta có BM \( \bot \) CH mà BM \( \bot \) OH nên BM \( \bot \) (OHC), do đó OC \( \bot \) BM, nhưng OC \( \bot \) AM nên OC \( \bot \) (ABM). Vậy OC \( \bot \)AB.
Điểm O thuộc đường cao OC và đường cao AE của tam giác ABC nên O là trực tâm của tam giác ABC.
Như vậy, khi \(M{\rm{ }} \in {\rm{ }}\Delta{\rm{ }}(M \ne A)\) thì H là trực tâm của tam giác MBC khi và chỉ khi H là hình chiếu của trực tâm O của tam giác ABC trên ME.
Vậy quỹ tích của H là đường tròn đường kính OE (bỏ hai điểm O, E) trong mặt phẳng trung trực của BC.
b) (h.108b).
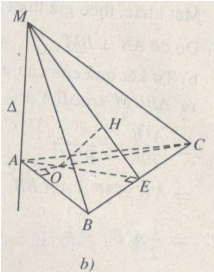
\({V_{OHBC}} = 2{V_{OHBE}} = {2 \over 3}{S_{OHE}}.BE\) (vì (OHE) là mặt phăng trung trực của BC) nên VOHBC lớn nhất khi và chỉ khi SOHE lớn nhất.
Tam giác vuông OHE có cạnh huyền OE cố định nên có diện tích lớn nhất khi và chỉ khi tam giác đó vuông cân, tức HEO = 45° hay AM = AE.
Vậy có hai vị trí của M trên \(\Delta \) để VOHBC đạt cực đại, đó là các điểm M sao cho AM = AE
