Cho khối lập phương ABCD.A’B’C’D’ cạnh bằng 1.
a) Tính góc tạo bởi các đường thẳng AC’ và A’B.
b) Gọi M, N, P lần lượt là trung điểm của các cạnh A’B’, BC, DD’. Chứng minh AC’ vuông góc với mặt phẳng (MNP).
c) Tính thể tích tứ diện AMNP.

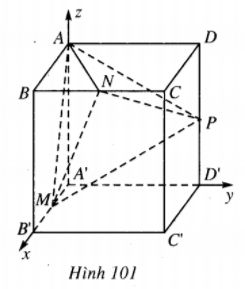
a) Ta chọn hệ trục Oxyz sao cho gốc O là đỉnh A’ của hình lập phương, tia Oy chứa A’B’, tia Oy chứa A’D’ và tia Oz chứa AA’. Khi đó
A’(0;0;0), B’(1;0;0);
D’(0;1;0), A=(0;0;1);
Advertisements (Quảng cáo)
C=(1;1;1), B=(1;0;1);
D=(0;1;1), C’(1;1;0).
Từ đó :
\(\eqalign{ & \overrightarrow {AC’} = (1;1; - 1),\overrightarrow {A’B} = (1;0;1) \cr & \Rightarrow \overrightarrow {AC’} .\overrightarrow {A’B} = 0 \Rightarrow AC’ \bot A’B. \cr} \)
b) Ta có
\(\eqalign{ & M = \left( {{1 \over 2};0;0} \right),N = \left( {1;{1 \over 2};1} \right),P = \left( {0;1;{1 \over 2}} \right). \cr & \overrightarrow {MN} = \left( {{1 \over 2};{1 \over 2};1} \right) \Rightarrow \overrightarrow {MN} .\overrightarrow {AC’} = 0 \cr&\Rightarrow MN \bot AC’. \cr & \overrightarrow {MP} = \left( { - {1 \over 2};1;{1 \over 2}} \right) \Rightarrow \overrightarrow {MP} .\overrightarrow {AC’} = 0 \cr&\Rightarrow MP \bot AC’. \cr & \cr} \)
Vậy \(AC’ \bot mp(MNP).\)
c) Ta có : \(\eqalign{ & \overrightarrow {MA} = \left( { - {1 \over 2};0;1} \right). \cr & \left[ {\overrightarrow {MN} ,\overrightarrow {MP} } \right] = \left( {\left| \matrix{ {1 \over 2} \hfill \cr 1 \hfill \cr} \right.\left. \matrix{ 1 \hfill \cr {1 \over 2} \hfill \cr} \right|;\left| \matrix{ 1 \hfill \cr {1 \over 2} \hfill \cr} \right.\left. \matrix{ {1 \over 2} \hfill \cr - {1 \over 2} \hfill \cr} \right|;\left| \matrix{ {1 \over 2} \hfill \cr - {1 \over 2} \hfill \cr} \right.\left. \matrix{ {1 \over 2} \hfill \cr 1 \hfill \cr} \right|} \right) \cr&= \left( { - {3 \over 4}; - {3 \over 4};{3 \over 4}} \right) \cr & \Rightarrow {V_{AMNP}} = {1 \over 6}\left| {\left[ {\overrightarrow {MN} ,\overrightarrow {MP} } \right].\overrightarrow {MA} } \right| \cr&\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;= {1 \over 6}.\left| {{9 \over 8}} \right| = {3 \over {16}}. \cr} \)
