Cho mặt phẳng . Bài 7 trang 6 Sách bài tập Hình học lớp 12 Nâng cao - Bài 2. Phép đối xứng qua mặt phẳng và sự bằng nhau của các khối đa diện
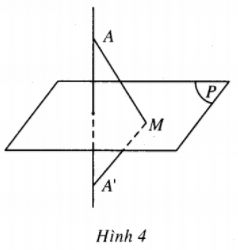
Cho mặt phẳng \(\left( P \right)\) và phép dời hình f có tính chất : f biến điểm M thành điểm M khi và chỉ khi M nằm trên \(\left( P \right)\). Chứng tỏ rằng f là phép đối xứng qua mặt phẳng \(\left( P \right)\).
(h.4) Phép dời hình f biến mọi điểm M nằm trên \(\left( P \right)\) thành chính nó . Với điểm A không nằm trên \(\left( P \right)\), ta gọi A’ là ảnh của A qua f . Khi đó, nếu \(M \in \left( P \right)\) thì \(MA = M{A’}\).
Advertisements (Quảng cáo)
Vậy \(\left( P \right)\) là mặt phẳng trung trực của AA’, tức A’ đối xứng với A qua \(\left( P \right)\).
Vậy f là phép đối xứng qua \(mp\left( P \right)\).
