Tìm các đường tiệm của đồ thị các hàm số sau:
a) \(y = {{2{x^2} + 1} \over {{x^2} - 2x}}\) b) \(y = {x \over {1 - {x^2}}}\)
c) \(y = {{{x^2}} \over {{x^2} - 1}}\) d) \(y = {{\sqrt x } \over {4 - {x^2}}}\)
Giải
a) Đường thẳng x = 0 là tiệm cận đứng của đồ thị (khi \(x \to {0^ + }\) và \(x \to {0^ - }\)).
Đường thẳng x = 2 là tiệm cận đứng của đồ thị (khi \(x \to {2^ + }\) và \(x \to {2^ - }\))
Đường thẳng y = 2 là tiệm cận ngang của đồ thị (khi \(x \to + \infty \) và \(x \to - \infty \))
b) Tiệm cận đứng: x = 1 (khi \(x \to {1^ + }\) và \(x \to {1^ - }\))
Advertisements (Quảng cáo)
Tiệm cận đứng: x = -1 (khi \(x \to {( - 1)^ + }\) và \(x \to {( - 1)^ - }\))
Tiệm cận ngang: y = 0 (khi \(x \to + \infty \) và \(x \to - \infty \))
c) Tiệm cận đứng: x = 1 (khi \(x \to {1^ + }\) và \(x \to {1^ - }\))
Tiệm cận đứng: x = -1 (khi \(x \to {( - 1)^ + }\) và \(x \to {( - 1)^ - }\))
Tiệm cận xiên: y = x (khi \(x \to + \infty \) và \(x \to - \infty \))
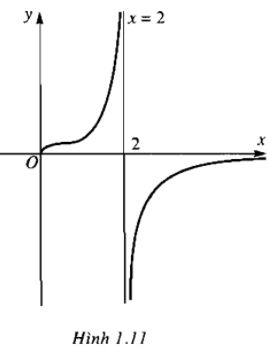
d) Tiệm cận đứng: x = 2 (khi \(x \to {2^ + }\) và \(x \to {2^ - }\))
Tiệm cận ngang: y = 0 (khi \(x \to + \infty \) ) (h.1.11)