Tìm tiệm cận đứng và tiệm cận ngang của đồ thị các hàm số sau:
a) \(y = {{x + 1} \over {2x + 1}}\)
b) \(y = 4 + {1 \over {x - 2}}\)
c) \(y = {{\sqrt {{x^2} + x} } \over {x - 1}}\)
d) \(y = {{\sqrt {x + 3} } \over {x + 1}}\)
Giải
a) Đường thẳng \(x = -{1 \over 2}\) là tiệm cận đứng của đồ thị (khi \(x \to {\left( { - {1 \over 2}} \right)^ - }\) và \(x \to {\left( { - {1 \over 2}} \right)^ + }\). Đường thẳng \(y = {1 \over 2}\) là tiệm cận ngang của đồ thị (khi \(x \to + \infty \) và \(x \to - \infty \))
b) Đường thẳng x = 2 là tiệm cận đứng của đồ thị (khi \(x \to {2^ - }\) và \(x \to {2^ + }\)). Đường thẳng y = 4 là tiệm cận ngang của đồ thị (khi \(x \to + \infty \) và \(x \to - \infty \))
Advertisements (Quảng cáo)
c) Vì \(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } {{x\sqrt {1 + {1 \over x}} } \over {x - 1}} = \mathop {\lim }\limits_{x \to + \infty } {{\sqrt {1 + {1 \over x}} } \over {1 - {1 \over x}}} = 1\)
\(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } {{ - x\sqrt {1 + {1 \over x}} } \over {x - 1}} = \mathop {\lim }\limits_{x \to - \infty } {{ - \sqrt {1 + {1 \over x}} } \over {1 - {1 \over x}}} = - 1\)
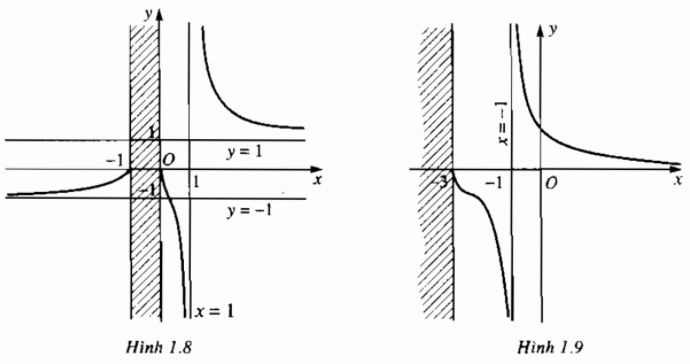
Nên đường thẳng y = 1 là tiệm cận ngang của đồ thị (khi \(x \to + \infty \)) và đường thẳng y = -1 là tiệm cận ngang của đồ thị (khi \(x \to - \infty \)) (h.1.8)
d) Đường thẳng x = -1 là tiệm cận ngang của đồ thị (khi \(x \to {( - 1)^ - }\) và \(x \to {( - 1)^ + }\)).
Đường thẳng y = 0 là tiệm cận ngang của đồ thị (khi \(x \to + \infty \)) (h1.1.9).
Baitapsgk.com
