Tìm tiệm cận đứng và tiệm cận xiên của đồ thị các hàm số sau:
a) \(y = 2x - 1 + {1 \over x}\) b) \(y = {{{x^2} + 2x} \over {x - 3}}\)
c) \(y = x - 3 + {1 \over {2{{(x - 1)}^2}}}\) d) \(y = {{2{x^2} + {x^2}} \over {{x^2} + 1}}\)
Giải
a) Đường thẳng x = 0 là tiệm cận đứng của đồ thị (khi \(x \to {0^ + }\) và \(x \to {0^ - }\).
Đường thẳng y = 2x – 1 là tiệm cận xiên của đồ thị (khi \(x \to + \infty \) và \(x \to - \infty \))
b) Đường thẳng x = 3 là tiệm cận đứng của đồ thị (khi \(x \to {3^ - }\) và \(x \to {3^ + }\)).
Đường thẳng y = x + 5 là tiệm cận xiên của đồ thị (khi \(x \to + \infty \) và \(x \to - \infty \))
Advertisements (Quảng cáo)
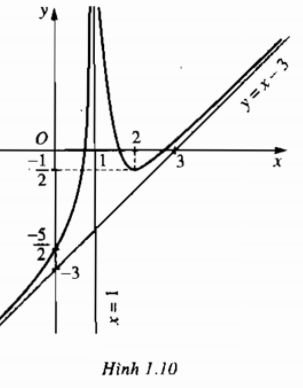
c) Vì \(\mathop {\lim }\limits_{x \to 1} y = + \infty \) nên đường thẳng x = 1 là tiệm cận đứng của đồ thị (khi \(x \to {1^ - }\) và \(x \to {1^ + }\)). Vì
\(y - (x - 3) = {1 \over {2{{(x - 1)}^2}}} \to 0\) khi \(x \to + \infty \) và \(x \to - \infty \)
nên đường thẳng y = x – 3 là tiệm cân xiên của đồ thị (khi \(x \to + \infty \) và \(x \to - \infty \)) (h.1.10).
d) Đường thẳng y = 2x – 1 là tiệm cận xiên của đồ thị (khi \(x \to + \infty \) và \(x \to - \infty \))
Có thể viết hàm số đã cho dưới dạng
\(y = 2x - 1 + {{1 - 2x} \over {{x^2} + 1}} \)
Vì hàm số xác định trên R nên đồ thị của nó không có tiệm cận đứng.
