
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:a) \(y = {x^3} - 12x + 1\) trên đoạn [-1;3] b) \(y = - {x^3} + 24{x^2} - 180x + 400\) trên đoạn [3;11]c) \(y = \frac{{2x + 1}}{{x - 2}}\) trên đoạn [3;7] d) \(y = \sin 2x\) trên đoạn \([0;\frac{{7\pi }}{{12}}]\)

Tìm đạo hàm, lập bảng biến thiên và xác định giá trị lớn nhất, giá trị nhỏ nhất của hàm số

a) Xét \(y = {x^3} - 12x + 1\) trên đoạn [-1;3]
\(y’ = 3{x^2} - 12 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = - 2(loai)\end{array} \right.\)
Bảng biến thiên:
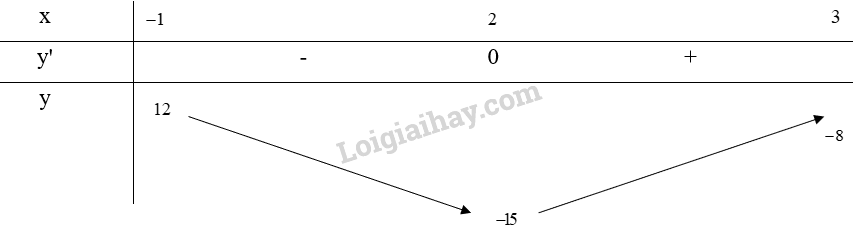
Từ bảng biến thiên, ta thấy \(\mathop {\max }\limits_{[ - 1;3]} y = y( - 1) = 12\) và \(\mathop {\min }\limits_{[ - 1;3]} y = y(2) = - 15\)
b) Xét \(y = - {x^3} + 24{x^2} - 180x + 400\) trên đoạn [3;11]
\(y’ = - 3{x^2} + 48x - 180 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 10\\x = 6\end{array} \right.\)
Bảng biến thiên:
Advertisements (Quảng cáo)
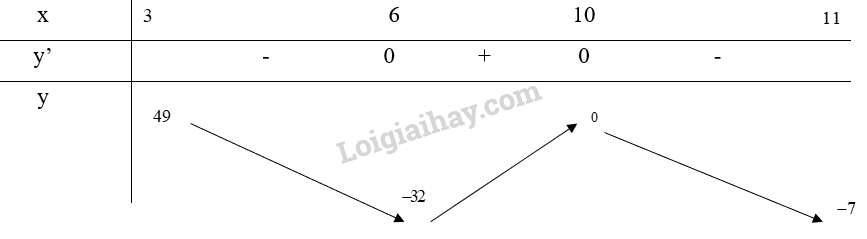
Từ bảng biến thiên, ta thấy \(\mathop {\max }\limits_{[3;11]} y = y(3) = 49\) và \(\mathop {\min }\limits_{[3;11]} y = y(6) = - 32\)
c) Xét \(y = \frac{{2x + 1}}{{x - 2}}\) trên đoạn [3;7]
\(y’ = \frac{{ - 5}}{{{{(x - 2)}^2}}} < 0\forall x \in [3;7]\)
Bảng biến thiên:
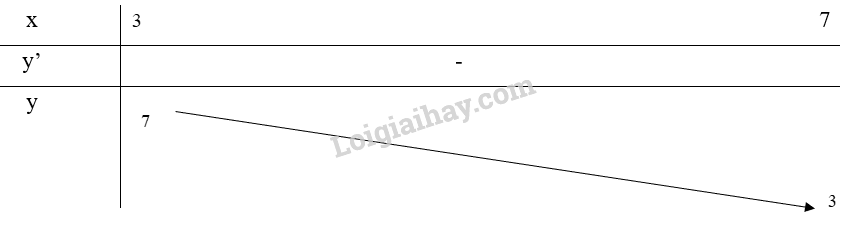
Từ bảng biến thiên, ta thấy \(\mathop {\max }\limits_{[3;7]} y = y(3) = 7\) và \(\mathop {\min }\limits_{[3;7]} y = y(7) = 3\)
d) Xét \(y = \sin 2x\) trên đoạn \([0;\frac{{7\pi }}{{12}}]\)
\(y’ = 2\cos 2x = 0 \Leftrightarrow 2x = \frac{\pi }{2} + k\pi \Leftrightarrow x = \frac{\pi }{4} + \frac{{k\pi }}{2}(k \in \mathbb{Z})\)
Ta có: \(x \in [0;\frac{{7\pi }}{{12}}] \Rightarrow k = 0 \Rightarrow x = \frac{\pi }{4}\)
Bảng biến thiên:
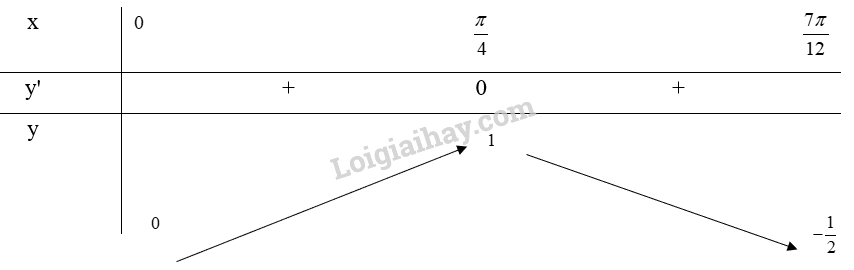
Từ bảng biến thiên, ta thấy \(\mathop {\max }\limits_{[0;\frac{{7\pi }}{{12}}]} y = y(\frac{\pi }{4}) = 1\) và \(\mathop {\min }\limits_{[0;\frac{{7\pi }}{{12}}]} y = y(\frac{{7\pi }}{{12}}) = - \frac{1}{2}\)
