
Tìm giá trị nhỏ nhất của các hàm số sau:a) \(y = {x^3} - 3x - 4\) trên nửa khoảng [-3;2) b) \(y = \frac{{3{x^2} - 4x}}{{{x^2} - 1}}\) trên khoảng \(( - 1; + \infty )\)

Tìm đạo hàm, lập bảng biến thiên và xác định giá trị nhỏ nhất

a) Xét \(y = {x^3} - 3x - 4\) trên nửa khoảng [-3;2)
\(y’ = 3{x^2} - 3 = 0 \Rightarrow \left[ \begin{array}{l}x = 1\\x = - 1\end{array} \right.\)
Bảng biến thiên:
Advertisements (Quảng cáo)
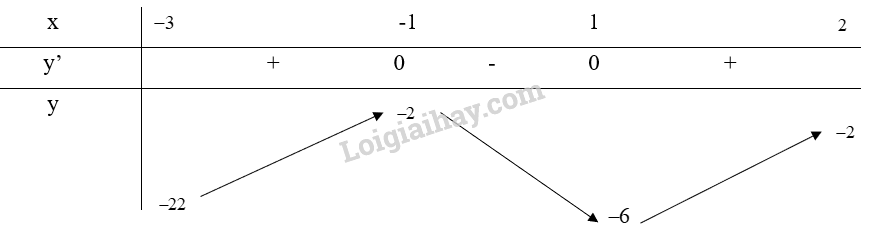
Từ bảng biến thiên, ta thấy \(\mathop {\min }\limits_{[ - 3;2)} y = y( - 3) = - 22\)
b) Xét \(y = \frac{{3{x^2} - 4x}}{{{x^2} - 1}}\) trên khoảng \(( - 1; + \infty )\)
Tập xác định: \(D = ( - 1; + \infty )\backslash \{ 1\} \)
\(y’ = \frac{{4{x^2} - 6x + 4}}{{{{({x^2} - 1)}^2}}} > 0\forall x \in D\)
Bảng biến thiên:
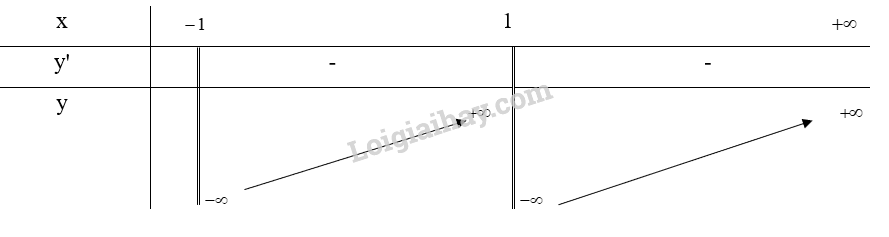
Từ bảng biến thiên, ta thấy hàm số không tồn tại giá trị nhỏ nhất trên khoảng \(( - 1; + \infty )\)
