Với các giá trị nào của a hàm số nghịch biến trên R. Bài 4 trang 8 SGK Đại số và Giải tích 12 Nâng cao - Bài 1. Tính đơn điệu của hàm số
Bài 4. Với các giá trị nào của a hàm số \(y = ax - {x^3}\) nghịch biến trên \(\mathbb R\)
Tập xác định \(D=\mathbb R\)
\(y’ = a - 3{x^2}\)
• Nếu \(a < 0\) thì \(y’ < 0\) với mọi \(x \in {\mathbb R}\), khi đó hàm số nghịch biến trên \(\mathbb R\).
• Nếu \(a = 0\) thì \(y’ = - 3{x^2} \le 0\) với mọi \(x \in {\mathbb R}\), \(y’=0\Leftrightarrow x=0\).
Advertisements (Quảng cáo)
Vậy hàm số nghịch biến trên \(\mathbb R\).
• Nếu \(a > 0\) thì \(y’ = 0\) \( \Leftrightarrow x = \pm {\sqrt {a \over 3}}\)
Ta có bảng biến thiên
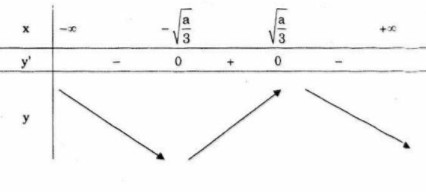
Trong trường hợp này, hàm số không đồng biến trên \({\mathbb R}\)
Vậy hàm số nghịch biến trên \({\mathbb R}\) khi và chỉ khi \(a \le 0\).