Cho hàm số \(f(x) = {4 \over \pi }x - \tan x,x \in \left[ {0;{\pi \over 4}} \right]\)
a) Xét chiều biến thiên của hàm số trên đoạn \(\left[ {0;{\pi \over 4}} \right]\)
b) Từ đó suy ra rằng: \(\tan x \le {4 \over \pi }x\) với mọi \(x \in \left[ {0;{\pi \over 4}} \right]\)
Giải
a) Hàm số f liên tục tên nửa khoảng \(\left[ {0;{\pi \over 4}} \right]\) và có đạo hàm
\(f'(x) = {4 \over \pi } - {1 \over {{{\cos }^2}x}} = {{4 - \pi } \over \pi } - {\tan ^2}x,x \in \left( {0;{\pi \over 4}} \right)\)
\(f'(x) = 0 \Leftrightarrow \tan x = \sqrt {{{4 - \pi } \over \pi }} \)
Advertisements (Quảng cáo)
Dễ dàng thấy rằng \(0 < \sqrt {{{4 - \pi } \over \pi }} < 1 = \tan {\pi \over 4}\). Do đó tồn tại một số duy nhất \(\alpha \in \left( {0;{\pi \over 4}} \right)\) sao cho \(\tan \alpha = \sqrt {{{4 - \pi } \over \pi }} \)
Bảng biến thiên
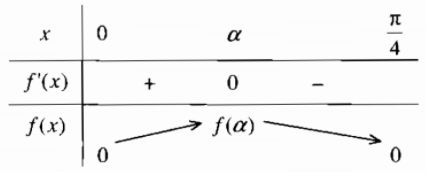
Hàm số đồng biến trên đoạn \(\left[ {0;\alpha} \right]\) và nghịch biến trên \(\left[ {\alpha ;{\pi \over 4}} \right]\)
b) Theo bảng biến thiên ta có
\(f(x) \ge 0\) với mọi \(x \in \left[ {0;{\pi \over 4}} \right]\)
Từ đó có bất đẳng thức cần chứng minh.
