Bài 6. Cho hàm số \(y = {{mx - 1} \over {2x + m}}\) .
a) Chứng minh rằng với mọi giá trị của tham số \(m\), hàm số luôn đồng biến trên mỗi khoảng xác định của nó.
b) Xác định m để tiệm cận đứng đồ thị đi qua \(A(-1 ; \sqrt2)\).
c) Khảo sát sự biến thiên và vẽ đồ thị của hàm số khi \(m = 2\).

a) \(y = {{mx - 1} \over {2x + m}}\).
Tập xác định: \(\mathbb R\backslash \left\{ {{{ - m} \over 2}} \right\}\) ;
\(y’ = {{{m^2} + 2} \over {{{(2x + m)}^2}}} > 0,\forall x \ne - {m \over 2}\)
Do đó hàm số luôn đồng biến trên mỗi khoảng xác định của nó.
b) Tiệm cận đứng \(∆\) : \(x = - {m \over 2}\).
\(A(-1 ; \sqrt2) ∈ ∆\) \(⇔- {m \over 2}= -1 ⇔ m = 2\).
c) \(m = 2\) thì hàm số đã cho có phương trình là:
\(y = {{2x - 1} \over {2x + 2}}\).
Tập xác đinh: \(D=\mathbb R\backslash {\rm{\{ }} - 1\} \)
* Sự biến thiên:
Advertisements (Quảng cáo)
\(y’ = {6 \over {{{(2x + 2)}^2}}} > 0\forall x \in D\)
- Hàm số đồng biến trên khoảng: \((-\infty;-1)\) và \((-1;+\infty)\)
- Cực trị:
Hàm số không có cực trị.
- Tiệm cận:
\(\eqalign{
& \mathop {\lim y}\limits_{x \to \pm \infty } = 1 \cr
& \mathop {\lim y}\limits_{x \to - {1^ - }} = + \infty \cr
& \mathop {\lim y}\limits_{x \to - {1^ + }} = - \infty \cr} \)
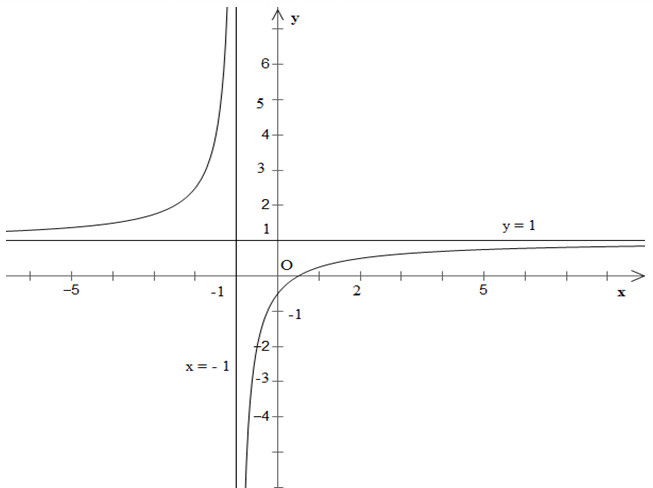
Tiệm cận đứng là \(x=-1\), tiệm cận ngang là: \(y=1\)
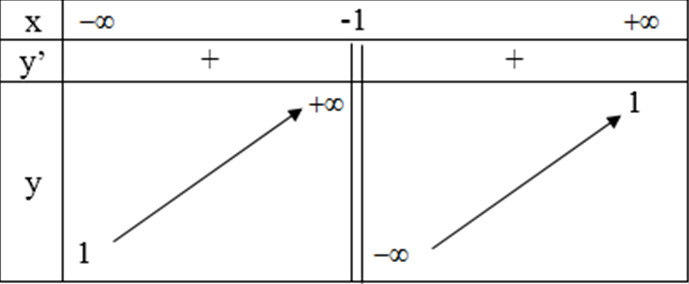
- Bảng biến thiên
* Đồ thị
Đồ thị hàm số giao \(Ox\) tại điểm \(({1\over 2};0)\), giao \(Oy\) tại điểm \((0;{-1\over 2})\).
Đồ thị hàm số nhận điểm \(I(-1;1)\) làm tâm đối xứng.