Lý thuyết hàm số mũ, hàm số lôgarit: Bài 4. Hàm số mũ hàm số lôgarit...

1. Định nghĩa

Hàm số mũ là hàm số có dạng y= a^x, hàm số lôgarit là hàm số có dạng  y = log_ax ( với cơ số a dương khác 1).

2. Tính chất của hàm số mũ y= a^x ( a > 0, a# 1).

- Tập xác định: \(\mathbb{R}\).

- Đạo hàm: ∀x ∈ \(\mathbb{R}\),y^’= a^xlna.

- Chiều biến thiên          

    +) Nếu a> 1 thì hàm số luôn đồng biến

    +) Nếu 0< a < 1 thì hàm số lôn nghịch biến

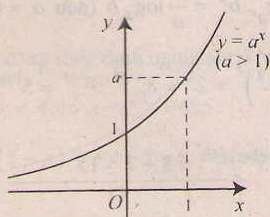
- Tiệm cận: trục Ox là tiệm cận ngang.

- Đồ thị nằm hoàn toàn về phía trên trục hoành (  y= a^x  > 0, ∀x), và luôn cắt trục tung taih điểm ( 0;1) và đi qua điểm (1;a).

3. Tính chất của hàm số lôgarit y = log_ax (a> 0, a# 1).

- Tập xác định: (0; +∞).

- Đạo hàm ∀x ∈ (0; +∞),y^’ = \(\frac{1}{xlna}\).

- Chiều biến thiên:  

    +) Nếu a> 1 thì hàm số luôn đồng biến

     +) Nếu 0< a < 1 thì hàm số luôn nghịch biến

- Tiệm cận: Trục Oy là tiệm cận đứng.

- Đồ thị nằm hoàn toàn phía bên phải trục tung, luôn cắt trục hoành tại điểm (1;0) và đi qua điểm (a;1).

4. Chú ý 

- Vì e > 1 nên nếu a > 1 thì lna > 0, suy ra (a^x)^’ > 0,∀x và (log_ax)^’ > 0, ∀x > 0; 

do đó hàm số mũ và hàm số lôgarit với cơ số lớn hơn 1 đều là những hàm số luôn luôn đồng biến.

Tương tự, nếu 0 < a< 1thì lna < 0, (a^x)^’ < 0 và (log_ax)^’ < 0, ∀x > 0; hàm số mũ và hàm số lôgarit với cơ số nhỏ hơn 1 đều là những hàm số luôn luôn nghịch biến.

- Công thức đạo hàm của hàm số lôgarit có thể mở rộng thành

    (ln|x|)^’  = \(\frac{1}{x}\), ∀x # 0 và (log_a|x|)^’ = \(\frac{1}{xlna}\), ∀x\(\ne\) 0.