
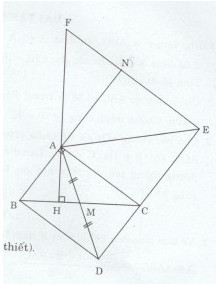
Cho tam giác ABC vuông tại A (AB < AC). Gọi M là trung điểm của BC. Tên tia đối của tia MA lấy điểm D sao cho MD = MA. Trên tia đối của tia CD lấy điểm E sao cho CE = CA.
a) Chứng minh rằng tam giác ACE vuông cân.
b) Kẻ AH vuông góc với BC. Đường thẳng kẻ từ E song song với AC cắt đường thẳng AH tại F. Chứng minh rằng AF = BC.

a)Xét tam giác AMC và DMB ta có:
AM = DM (giả thiết)
\(\widehat {AMC} = \widehat {DMB}\) (hai góc đối đỉnh)
MC = MB (M là trung điểm của BC)
Do đó: \(\eqalign{ & \Delta AMC = \Delta DMB(c.g.c) \cr & \Rightarrow \widehat {ACM} = \widehat {MBD} \cr} \)
Mà hai góc ACM và MBD so le trong nên AC // BD.
Ta có: \(BA \bot AC(\Delta ABC\) vuông tại A)
AC // BD (chứng minh trên)
\(\Rightarrow CD \bot AC\)
Vậy tam giác ACE vuông tại C.
Advertisements (Quảng cáo)
Ta có: tam giác ACE vuông tại C có: CA = CE (giả thiết)
Do đó: tam giác ACE vuông cân tại C.
b) Gọi N là giao điểm của AB và EF.
Ta có: EF // AC (gt), \(AB \bot AC(\widehat {BAC} = {90^0}) \Rightarrow AB \bot EF\)
Xét tam giác NAE vuông tại N và tam giác CEA vuông tại C có:
AE là cạnh chung.
\(\widehat {AEN} = \widehat {EAC}\) (so le trong và EF // AC)
Do đó: \(\Delta NAE = \Delta CEA\) (cạnh huyền - góc nhọn) => AN = CE.
Ta có: AN = CA (= CE).
Xét tam giác NFA và ABC có:
\(\widehat {FNA} = \widehat {BAC}( = {90^0})\)
AN = CA
\(\widehat {NAF} = \widehat {ACB}\) (cùng phụ với góc HAC)
Do đó: \(\Delta NFA = \Delta ABC(g.c.g)\) . Vậy AF = BC.
