
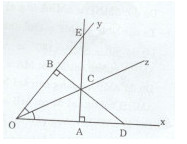
Cho góc nhọn xOy, Ot là tia phân giác của góc xOy. Trên tia Ot lấy điểm C, kẻ \(CA \bot Ox(A \in Ox)\), kẻ \(CB \bot Oy(B \in Oy).\)
a) Chứng minh rằng CA = CB.
b) Gọi D là giao điểm của BC và Ox, E là giao điểm của AC và Oy. So sánh độ dài CE và CD.
c) Biết OC = 17 cm, OB = 15 cm. Tính BC.

a)Xét tam giác OCA vuông tại A và tam giác OCB vuông tại B ta có:
OC là cạnh chung.
\(\widehat {COA} = \widehat {BOA}\) (Ot là tia phân giác của góc xOy)
Advertisements (Quảng cáo)
Do đó: \(\Delta OCA = \Delta OCB\) (cạnh huyền - góc nhọn)
=>CA = CB.
b) Xét tam giác ACD và BCE ta có:
\(\eqalign{ & AC = BC(\Delta OCA = \Delta OCB) \cr & \widehat {CAD} = \widehat {CBE}( = {90^0}) \cr} \)
\(\widehat {ACD} = \widehat {BCE}\) (hai góc đối đỉnh)
Do đó: \(\Delta ACD = \Delta BCE(g.c.g) \Rightarrow CD = CE\)
c) Tam giác OBC vuông tại B \(\Rightarrow O{B^2} + B{C^2} = O{C^2}\) (định lý Pythagore)
Do đó: \({15^2} + B{C^2} = {17^2} \Rightarrow B{C^2} = {17^2} - {15^2} = 289 - 225 = 64\)
Mà BC > 0. Do đó: \(BC = \sqrt {64} = 8(cm).\)
