
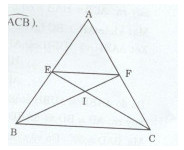
Cho tam giác ABC cân tại A. Tia phân giác của góc B cắt tại F, tia phân giác của góc C cắt AB tại E.
a) Chứng minh rằng \(\widehat {ABF} = \widehat {ACE}.\)
b) Chứng minh rằng tam giác AEF cân.
c) Gọi I là giao điểm của BF và CE. Chứng minh rằng tam giác IBC và IEF là những tam giác cân.

a)Ta có: \(\widehat {FBC} = \widehat {ABF} = {{\widehat {ABC}} \over 2}\) (BF là tia phân giác của góc ABC)
\(\widehat {ECB} = \widehat {ACE} = {{\widehat {ACB}} \over 2}\) (CE là tia phân giác của góc ACB)
\(\widehat {ABC} = \widehat {ACE}(\Delta ABC\) cân tại A)
Do đó: \(\widehat {ABF} = \widehat {FBC} = \widehat {ECB} = \widehat {ACE} \Rightarrow \widehat {ABF} = \widehat {ACE}\)
Advertisements (Quảng cáo)
b)Xét tam giác AEC và AFB có:
\(\widehat {EAC} = \widehat {FAB}\) (góc chung)
AC = AB (tam giác ABC cân tại A)
\(\widehat {ACE} = \widehat {ABF}\) (chứng minh câu a)
Do đó: \(\Delta AEC = \Delta AFB(g.c.g) \Rightarrow AE = AF.\) Vậy \(\Delta AEF\) cân tại A.
c) Ta có: \(\widehat {IBC} = \widehat {ICB}\) (chứng minh câu a). Vậy tam giác IBC cân tại I.
Ta có: \(\widehat {AEF} + \widehat {IEF} = \widehat {AEI};\widehat {AFE} + \widehat {IFE} = \widehat {AFI}\)
Mà \(\widehat {AEF} = \widehat {AFE};\widehat {AEI} = \widehat {AFI} \Rightarrow \widehat {IEF} = \widehat {IFE}\)
Do đó tam giác IEF cân tại I.
