
Cho tam giác ABC cân tại C có CA = CB = 10 cm, AB = 12 cm. Kẻ \(CM \bot AB(M \in AB).\)
a) Chứng minh rằng MA = MB.
b) Tính độ dài CM.
c) Kẻ \(MK \bot BC(K \in BC),MH \bot AC.\) Chứng minh rằng MK = MH.

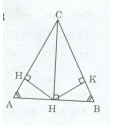
a)Xét tam giác AMC vuông tại M và tam giác BMC vuông tại M ta có:
AC = BC (tam giác ABC cân tại C)
\(\widehat {CAM} = \widehat {CBM}(\Delta ABC\) cân tại C)
Do đó: \(\Delta AMC = \Delta BMC\) (cạnh huyền - góc nhọn) => MA = MB.
Advertisements (Quảng cáo)
b) Ta có: \(MA = MB = {{AB} \over 2} = {{12} \over 2} = 6(cm)\)
Tam giác AMC vuông tại M có: \(M{A^2} + M{C^2} = A{C^2}\) (định lí Pythagoare).
Do đó: \({6^2} + M{C^2} = {10^2} \Rightarrow M{C^2} = {10^2} - {6^2} = 100 - 36 = 64.\)
Mà MC > 0 nên \(MC = \sqrt {64} = 8(cm)\)
c) Xét tam giác AMH vuông tại H và tam giác MBK vuông tại K ta có:
AM = BM (chứng minh câu a)
\(\widehat {HAM} = \widehat {KBM}(\Delta ABC\) cân tại C)
Do đó: \(\Delta AMH = \Delta BMK\) (cạnh huyền - góc nhọn) => MH = MK.
Vậy MK = MH.
