Bài tập - Chủ đề 5 : Quan hệ giữa các yếu tố trong tam giác - Bài tập 17 trang 97 Tài liệu dạy – học Toán 7 tập 2. Giải bài tập Cho tam giác DEF, I là trung điểm của EF. Kẻ EH vuông góc với DI tại H, FK vuông góc với DI.
Cho tam giác DEF, I là trung điểm của EF. Kẻ EH vuông góc với DI tại H, FK vuông góc với DI.
a) Chứng minh IH = IK
b) Chứng minh DE + DF > DH + DK
c) Chứng minh DH + DKL = 2DI
d) Chứng minh DE + DF > 2DI.
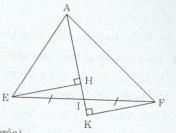
a) Xét ∆EHI vuông tại H và ∆IFK vuông tại K ta có:
EI = IF (I là trung điểm của EF)
Và \(\widehat {EIH} = \widehat {KIF}\) (hai góc đối đỉnh)
Do đó ∆EHI = ∆FKI (cạnh huyền – góc nhọn)
Advertisements (Quảng cáo)
=> IH = KI.
b) Ta có DE > DH (đường xiên lớn hơn đường vuông góc)
Và DF > DK (đường xiên lớn hơn đường vuông góc)
Suy ra DE + DF > DH + DK.
c) Ta có IK = HI. Do đó
DH + DK = DH + IK + DI
= DH + HI + DI = (DH + HI) + DI
= DI + DI = 2DI
d) Ta có DE + DF > DH + DK (câu b) và
DH + DK = 2DI (câu c)
Nên DE + DF > 2DI.