Bài tập - Chủ đề 5 : Quan hệ giữa các yếu tố trong tam giác - Bài tập 19 trang 97 Tài liệu dạy – học Toán 7 tập 2. Giải bài tập Cho tam giác ABC nhọn có AB < AC, kẻ AH vuông góc với BC (H thuộc BC). Gọi M là điểm nằm giữa A và H, tia BM cắt AC ở D.
Cho tam giác ABC nhọn có AB < AC, kẻ AH vuông góc với BC (H thuộc BC). Gọi M là điểm nằm giữa A và H, tia BM cắt AC ở D.
a) Chứng minh BM < CM
b) Chứng minh DM < DH
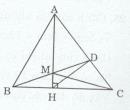
a) Ta có BH, CH lần lượt là hình chiếu của đường xiên AB, AC trên đường thẳng BC và AB < AC (gt).
=> BH < CH (quan hệ giữa đường xiên và hình chiếu)
Advertisements (Quảng cáo)
Mặt khác BH, CH lần lượt là hình chiếu của đường xiên BM, CM trên đường thẳng BC và BH < CH.
=> BM < CM (quan hệ giữa hình chiếu và đường xiên).
b) \(\widehat {DMH} > \widehat {BHM} = 90^\circ (\widehat {DMH}\) là góc ngoài của tam giác BMH)
∆DMH có \(\widehat {DMH}\) tù =>\(\widehat {DMH}\) là góc lớn nhất trong ba góc
=> DH là cạnh lớn nhất trong ba cạnh (quan hệ giữa góc và cạnh trong một tam giác)
Vậy DM < DH.