
Cho tứ giác \(ABCD\) có \(\widehat C = \widehat D\) và \(AD = BC\). Chứng minh tứ giác \(ABCD\) là hình thang cân.

Dựa vào tính chất của hình thang cân:
Trong một hình thang cân
- Hai cạnh bên bằng nhau
- Hai đường chéo bằng nhau.

Advertisements (Quảng cáo)
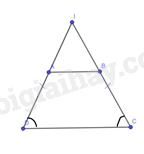
Gọi \(I\) là giao điểm của \(AD\) và \(BC\)
Do \(\widehat C = \widehat D\) nên tam giác \(ICD\) cân tại \(I\). Suy ra \(ID = IC\)
Mà \(AD = BC\), suy ra \(IA = IB\). Do đó, tam giác \(IAB\) cân tại \(I\).
Vì hai tam giác \(IAB\) và \(ICD\) đều cân tại \(I\) nên
\(\widehat {IAB} = \widehat D\) (cùng bằng \(\frac{{180^\circ - \widehat I}}{2}\))
Mà \(\widehat {IAB}\) và \(\widehat D\) nằm ở vị trí đồng vị, suy ra \(AB//CD\)
Tứ giác \(ABCD\) có \(AB//CD\) và \(\widehat C = \widehat D\) nên \(ABCD\) là hình thang cân.
