
Cho hình vuông \(ABCD\). Lấy điểm \(E\) thuộc cạnh \(CD\) và điểm \(F\) thuộc tia đối của tia \(BC\) sao cho \(BF = DE\).
a) Chứng minh tam giác \(AEF\) là tam giác vuông cân
b) Gọi \(I\) là trung điểm của \(EF\). Trên tia đối của tia \(IA\) lấy điểm \(K\) sao cho \(IK = IA\). Chứng minh tứ giác \(AEKF\) là hình vuông.
c) Chứng minh \(I\) thuộc đường thẳng \(BD\).

Trong một hình vuông,
- Các cạnh đối song song
- Hai đường chéo bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.
- Hai đường chéo là các đường phân giác của các góc ở đỉnh.

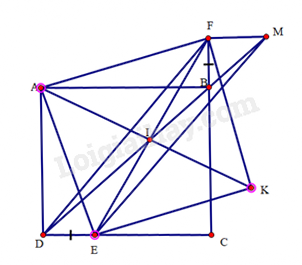
Từ điểm \(F\) kẻ đường thẳng song song với \(CD\) cắt đường thẳng \(BD\) tại \(M\)
a) \(\Delta ADE = \Delta ABF\) (c.g.c)
Advertisements (Quảng cáo)
Suy ra \(AE = AF\) và \(\widehat {DAE} = \widehat {BAF}\)
Suy ra \(\widehat {DAE} + \widehat {BAE} = \widehat {BAF} + \widehat {BAE}\) hay \(\widehat {BAD} = \widehat {EAF}\).
Do đó, \(\widehat {EAF} = 90^\circ \)
Tam giác \(AEF\) có \(\widehat {EAF} = 90^\circ ,AE = AF\) nên tam giac \(AEF\) vuông cân tại \(A\).
b) Tứ giác \(AEKF\) có hai đường chéo \(AK,EF\) cắt nhau tại trung điểm \(I\) của mỗi đường nên \(AEKF\) là hình bình hành
hình bình hành \(AEKF\) có \(\widehat {EAF} = 90^\circ \) nên \(AEKF\) là hình chữ nhật.
hình chữ nhật \(AEKF\) có \(AE = AF\) nên \(AEKF\) là hình vuông.
c) Do \(ABCD\) là hình vuông nên ta tính được \(\widehat {CBD} = 45^\circ \). Mà \(\widehat {FBM} = \widehat {CBD}\) (hai góc đối đỉnh), suy ra \(\widehat {FBM} = 45^\circ \).
Do \(MF = CD\) nên \(\widehat {BFM} = \widehat {BCD}\) (cặp góc so le trong)
Do đó \(\widehat {BFM} = 90^\circ \). Ta chứng minh được tam giác \(FBM\) vuông cân tại \(F\). Suy ra \(MF = BF\). Mà \(BF = DE\), suy ra \(MF = DE\).
Tứ giác \(D\`E M\) có \(MF = DE\) và \(MF//DE\) nên \(D\`E M\) là hình bình hành.
Mà \(I\) là trung điểm của \(EF\), suy ra \(I\) là trung điểm của \(DM\)
Vậy \(I\) thuộc đường thẳng \(DM\) hay \(I\) thuộc đường thẳng \(BD\).
