Dựa vào bất đẳng thức tam giác: trong một tam giác, tổng độ dài của hai cạnh bât kì luôn lớn hơn độ dài cạnh còn lại. Gợi ý giải bài 9 trang 90 sách bài tập toán 8 - Cánh diều - Bài 2. Tứ giác. Chứng minh rằng: Trong một tứ giác,...

Chứng minh rằng: Trong một tứ giác, tổng độ dài hai đường chéo lớn hơn tổng độ dài hai cạnh đối.

Dựa vào bất đẳng thức tam giác: trong một tam giác, tổng độ dài của hai cạnh bât kì luôn lớn hơn độ dài cạnh còn lại.

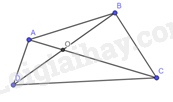
Gọi \(O\) là giao điểm của hai đường chéo \(AC\) và \(BD\) trong tứ giác \(ABCD\).
Advertisements (Quảng cáo)
Xét tam giác \(OAB\), ta có: \(OA + OB > AB\)
Xét tam giác \(OCD\), ta có: \(OC + OD > CD\)
Suy ra \(OA + OB + OC + OD > AB + CD\)
Hay \(AC + BD > AB + CD\)
Tương tự ta cũng chứng minh được \(AC + BD > AD + BC\)
Vậy: Trong một tứ giác, tổng độ dài hai đường chéo lớn hơn tổng độ dài hai cạnh đối.
