Advertisements (Quảng cáo)
Giả sử AC là đường chéo lớn của hình bình hành ABCD. Từ C, vẽ đường vuông góc CE với đường thẳng AB, đường vuông góc CF với đường thẳng AD (E,F thuộc phần kéo dài của các cạnh AB và AD). Chứng minh rằng AB.AE + AD.AF = \(A{C^2}\).
Giải:
(hình trang 123 sgbt)
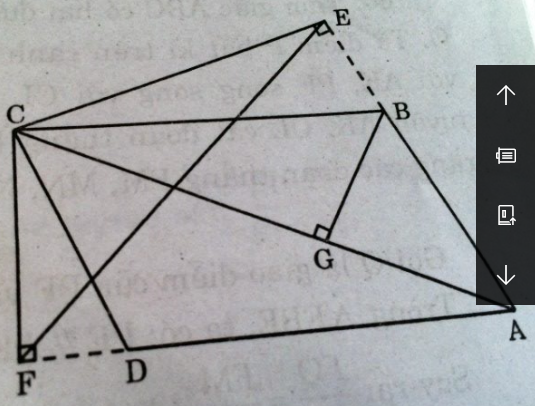
Dựng BG ⊥ AC.
Xét ∆ BGA và ∆ CEA, ta có:
\(\widehat {BGA} = \widehat {CEA} = 90^\circ \)
\(\widehat A\) chung
Suy ra: ∆ BGA đồng dạng ∆ CEA (g.g)
Suy ra: \({{AB} \over {AC}} = {{AG} \over {AE}}\)
Suy ra: AB.AE = AC.AG (1)
Xét ∆ BGC và ∆ CFA, ta có:
Advertisements (Quảng cáo)
\(\widehat {BGC} = \widehat {CFA} = 90^\circ \)
\(\widehat {BCG} = \widehat {CAF}\) (so le trong vì AD // BC)
Suy ra: ∆ BGC đồng dạng ∆ CFA (g.g)
Suy ra: \({{AF} \over {CG}} = {{AC} \over {BC}} \Rightarrow BC.AF = AC.CG\)
Mà BC = AD (tính chất hình bình hành )
Suy ra: AD.AF = AC.CG (2)
Cộng từng vế của đẳng thức (1) và (2) ta có:
AB.AE + AD.AF = AC.AG + AC.CG
\( \Rightarrow AB.AE + AD.AF = AC\left( {AG + CG} \right)\)
Mà \(AG + CG = AC\) nên \(AB.AE + AD.AF = A{C^2}\)
Mục lục môn Toán 8 (SBT)