Câu 59 trang 98 Sách bài tập Toán 8 tập 2: Chứng minh hai tam giác DEC và ABC là hai tam giác đồng...

Tam giác ABC có hai đường cao là AD và BE (D thuộc BC, E thuộc AC).

Chứng minh hai tam giác DEC  và ABC là hai tam giác đồng dạng.

Giải:

(hình trang 124 sgbt)

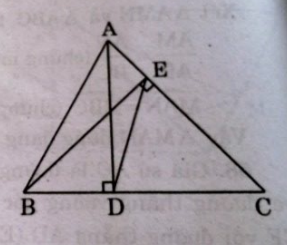
Xét ∆ ADC và ∆ BEC, ta có:

$\widehat {ADC} = \widehat {BEC} = 90^\circ$

$\widehat C$  chung

Suy ra: ∆ ADC đồng dạng ∆ BEC (g.g)

Suy ra: ${{AC} \over {BC}} = {{DC} \over {EC}} \Rightarrow {{EC} \over {BC}} = {{DC} \over {AC}}$

Xét ∆ DEC và ∆ ABC, ta có:

${{EC} \over {BC}} = {{DC} \over {AC}}$

$\widehat C$ chung

Vậy ∆ DEC đồng dạng ∆ ABC (c.g.c)