
a) Hình a, cho biết \(\Delta MNP \sim \Delta EFC\) . Viết dãy tỉ số đồng dạng và chỉ ra các cặp góc tương ứng.
b) Hình b, cho biết \(\Delta ABC \sim \Delta DEF\). Tính số đo \(\widehat D\,\,\,\& \,\,\,\widehat F\)
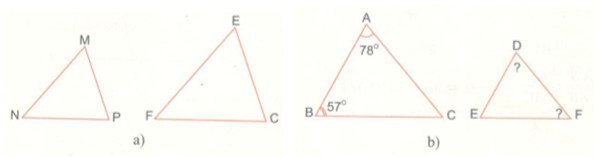

a) Ta có \(\Delta MNP \sim \Delta EFC\) khi đó:
\(\eqalign{ & {{MN} \over {EF}} = {{MP} \over {EC}} = {{NP} \over {FC}} \cr & \widehat M = \widehat E,\widehat N = \widehat F,\widehat P = \widehat C \cr & b)\Delta ABC \sim \Delta DEF \cr&\Rightarrow \widehat A = \widehat D,\widehat C = \widehat F \cr} \)
Advertisements (Quảng cáo)
Mà \(\widehat A = 78^\circ \) nên \(\widehat D = 78^\circ \)
∆ABC có \(\widehat C + \widehat A + \widehat B = 180^\circ \) (tổng ba góc trong một tam giác)
\( \Rightarrow \widehat C + 78^\circ + 57^\circ = 180^\circ \)
\(\Rightarrow \widehat C + 135^\circ = 180^\circ \Rightarrow \widehat C = 45^\circ \)
Mà \(\widehat F = \widehat C\) nên \(\widehat F = 45^\circ \)
