
Ở hình sau, tam giác ABC vuông tại A có đường cao AH.
a) Hãy chỉ ra các cặp tam giác đồng dạng. Với mỗi cặp hãy viết đúng thứ tự các đỉnh.
b) Cho biết AB = 6 cm, AC = 8 cm. Tính độ dài các đoạn thẳng BC, BH, AH.
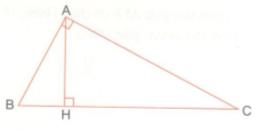

a) Xét ∆ABH và ∆ABC có: \(\widehat B\) chung và \(\widehat {AHB} = \widehat {BAC}( = 90^\circ ) \)
\(\Rightarrow \Delta ABH \sim \Delta CBA(g.g)\)
Xét ∆ABH và ∆AHC ta có: \(\widehat {AHB} = \widehat {AHC}( = 90^\circ )\) và \(\widehat {BAH} = \widehat {ACH}\) (cùng phụ với \(\widehat B)\)
\( \Rightarrow \Delta ABH \sim \Delta CAH(g.g)\)
∆ABE vuông tại A có: \(A{E^2} + A{B^2} = B{E^2}\) (định lý Py-ta-go)
Advertisements (Quảng cáo)
Xét ∆AHC và ∆ABC có: \(\widehat C\) chung và \(\widehat {AHC} = \widehat {BAC}( = 90^\circ )\)
\(\Rightarrow \Delta AHC \sim \Delta BAC(g.g)\)
b) ∆ABC vuông tại A có: \(B{C^2} = A{B^2} + A{C^2}\) (định lý Py-ta-go)
\( \Rightarrow B{C^2} = {6^2} + {8^2} = 100 \)
\(\Rightarrow BC = 10(cm)\)
\(\Delta ABH \sim \Delta CBA\) (câu a) \( \Rightarrow {{AB} \over {BC}} = {{AH} \over {CA}} = {{BH} \over {AB}} \)
\(\Rightarrow {6 \over {10}} = {{AH} \over 8} = {{BH} \over 6}\)
Từ đó suy ra:
\(\eqalign{ & {6 \over {10}} = {{AH} \over 8} \Rightarrow AH = 4,8(cm) \cr & {6 \over {10}} = {{BH} \over 6} \Rightarrow BH = 3,6(cm) \cr} \)
