Bài tập - Chủ đề 2 : Hình bình hành – Hình chữ nhật – Hình thoi – Hình vuông - Bài tập 25 trang 136 Tài liệu dạy – học Toán 8 tập 1. Giải bài tập Cho hình thoi ABCD, hai đường chéo AC và BD cắt nhau tại O. Biết AC = 6 cm, BD = 8 cm. Tính độ dài cạnh của hình thoi ABCD.
Cho hình thoi ABCD, hai đường chéo AC và BD cắt nhau tại O. Biết AC = 6 cm, BD = 8 cm. Tính độ dài cạnh của hình thoi ABCD.
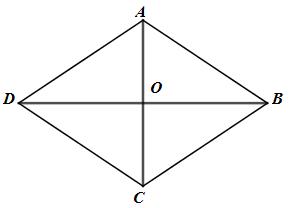
Hình thoi ABCD có hai đường chéo AC và BD cắt nhau tại O (gt)
\( \Rightarrow O\) là trung điểm của AC và BD
\( \Rightarrow AO = {{AC} \over 2}\) và \(DO = {{BD} \over 2}\)
Advertisements (Quảng cáo)
\( \Rightarrow AO = {6 \over 2} = 3\,\,\left( {cm} \right)\) và \(DO = {8 \over 2} = 4\,\,\left( {cm} \right)\)
\(AC \bot BD\) tại O (vì ABCD là hình thoi)
\(\Delta ADO\) vuông tại O có \(A{D^2} = A{O^2} + D{O^2}\) (Định lí Pytago)
\( \Rightarrow A{D^2} = {3^2} + {4^2} = 25 \Rightarrow AD = 5\) (cm)
Vậy \(AB = BC = DC = AD = 5\,\,\left( {cm} \right)\)