
Cho tứ giác ABCD có AB = BC và CA là tia phân giác của góc BCD. Đường thẳng vuông góc với AC tại A cắt đường thẳng CD ở E. Gọi M là trung điểm của AC.
a) Chứng minh rằng tứ giác ABCD là hình thang.
b) Chứng minh rằng tứ giác ABME là hình thang.

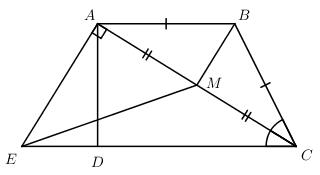
a) Ta có: \(AB = BC\,\,\left( {gt} \right) \Rightarrow \Delta ABC\) cân tại B \( \Rightarrow \widehat {BCA} = \widehat {BAC}\)
Mà \(\widehat {BCA} = \widehat {ACD}\) (CA là phân giác của \(\widehat {DCB}\))
Nên \(\widehat {BAC} = \widehat {ACD}\)
Advertisements (Quảng cáo)
Lại có \(\widehat {BAC}\) và \(\widehat {ACD}\) là hai góc so le trong.
Do đó AB // CD
Vậy tứ giác ABCD là hình thang.
b) ∆ABC cân tại B có BM là đường trung tuyến (M là trung điểm của AC)
=> BM cũng là đường cao của ∆ABC \( \Rightarrow BM \bot AC\)
Mà \(AE \bot AC(gt)\) nên BM // AC
Vậy tứ giác ABME là hình thang.
