Luyện tập - Chủ đề 1 : Tứ giác – Hình thang - Luyện tập 3 trang 106 Tài liệu dạy – học Toán 8 tập 1. Giải bài tập Cho tứ giác ABCD, gọi O là giao điểm của AC và BD. Biết rằng OA = OB, OC = OD. Chứng minh rằng tứ giác ABCD là hình thang cân.
Cho tứ giác ABCD, gọi O là giao điểm của AC và BD. Biết rằng OA = OB, OC = OD. Chứng minh rằng tứ giác ABCD là hình thang cân.
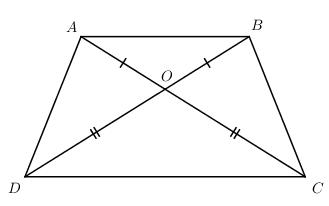
OA = OB (gt) và OC = OD (gt) \( \Rightarrow OA + OC = OB + OD \Rightarrow AC = BD\)
Ta có OA = OB => ∆OAB cân tại O \( \Rightarrow \widehat {ABO} = {{180^\circ - \widehat {AOB}} \over 2}\)
Advertisements (Quảng cáo)
Mà \(\widehat {ODC} = {{180^\circ - \widehat {DOC}} \over 2}\) (∆DOC cân tại O vì OD = OC)
Và \(\widehat {AOB} = \widehat {DOC}\) (đối đỉnh) nên \(\widehat {ABO} = \widehat {ODC}\)
Lại có \(\widehat {ABO}\) và \(\widehat {ODC}\) là hai góc so le trong
Do đó AB // CD => Tứ giác ABCD là hình thang
Hình thang ABCD (AB // CD) có \(AC = BD\) nên là hình thang cân.