Luyện tập 2 trang 106 Tài liệu dạy – học Toán 8 tập 1, Cho tam giác ABC cân tại A. Trên các cạnh AB, AC lấy lần lượt các điểm D và E sao cho AD = AE....

Cho tam giác ABC cân tại A. Trên các cạnh  AB, AC lấy lần lượt các điểm D và E sao cho AD = AE.

a) Chứng minh rằng BDEC là hình thang cân.

b) Tính các góc của hình thang cân đó, biết $\widehat {BAC} = {40^o}$.

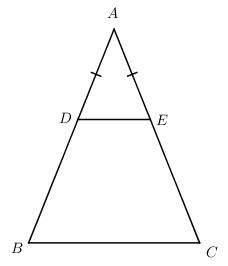
a) Ta có $AD = AE(gt) \Rightarrow \Delta ADE$ cân tại A $\Rightarrow \widehat {ADE} = {{180^\circ  - \widehat A} \over 2}$

Mà $\widehat B = {{180^\circ  - \widehat A} \over 2}$ (∆ABCcân tại A) nên $\widehat {ADE} = \widehat B$

Lại có $\widehat {ADE}$ và $\widehat B$ là hai góc đồng vị, do đó DE // BC

Vậy tứ giác BDEC là hình thang.

Hình thang BDEC (DE // BC) có $\widehat B = \widehat C$ (∆ABCcân tại A) nên là hình thang cân.

b) Ta có $\widehat B = {{180^\circ  - \widehat A} \over 2} = {{180^\circ  - 40^\circ } \over 2} = 70^\circ$

Mà $\widehat C = \widehat B$ (BDEC là hình thang cân) nên $\widehat B = \widehat C = 70^\circ$

Ta có : $\widehat B + \widehat {BDE} = 180^\circ$ (hai góc trong cùng phía và DE // BC)

$\Rightarrow 70^\circ  + \widehat {BDE} = 180^\circ  \Rightarrow \widehat {BDE} = 180^\circ  - 70^\circ  = 110^\circ$

Mà $\widehat {DEC} = \widehat {BDE}$ (BDEC là hình thang cân) nên $\widehat {BDE} = \widehat {DEC} = 110^\circ$