Dựng hình thang ABCD (AB// CD), biết ba cạnh: AD = 2cm, CD = 4 cm, BC = 3cm và đường chéo AC = 5 cm.
Hướng dẫn làm bài:
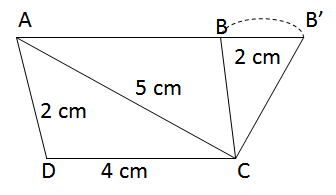
Dựng đoạn thẳng CD = 4cm.
-Dựng hai đường tròn (C; 5cm) và (D; 2cm) cắt nhau tại A.
-Dựng đường tròn (C; 2 cm) và đường tròn (A, 4cm) cắt nhau tại B.
Advertisements (Quảng cáo)
Đường thẳng AB kéo dài cắt đường tròn (C, 2cm) tại điểm B’ (ngoài điểm B đã kể trên).
Các tứ giác ABCD và AB’CD là những hình thang thỏa mãn đề bài.
Chứng minh: Vì B ∈(A, 4cm) nên AB = 4cm.
∆ABC = ∆DAC (AB = CD = 4 cm, AD = BC = 2cm, AC chung) do đó là cặp góc so le trong ta có: AB // CD.
Tứ giác ABCD có AB // CD, AD = 2cm, CD = 4 cm, BC = 2 cm là hình thang thỏa mãn yêu cầu, AB’CD cũng là hình thang thỏa mãn yêu cầu vì AB’//CD, AD = 2cm, CD = 4 cm, CB’ = 2 cm).
