
Cho đường tròn (O) có đường kính AB cố định. CD là một đường kính di động của (O). Các đường thẳng AC, AD cắt tiếp tuyến với (O) tại B lần lượt tại P và Q.
a) Chứng minh CPQD là tứ giác nội tiếp.
b) Chứng minh trung tuyến AI của tam giác APQ vuông góc với đường thẳng CD.
c) Xác định vị trí của CD để diện tích tứ giác CPQD bằng ba lần diện tích tam giác ACD.
a) Chứng minh \(\widehat {ADC} = \widehat {BPC}\), từ đó chứng minh tứ giác CPQD có tổng hai góc đối bằng 1800.
b) Gọi \(E = AI \cap CD\), chứng minh tam giác AED có tổng hai góc nhọn bằng 900.
c) \({S_{CPQD}} = 3{S_{ACD}} \Rightarrow {S_{APQ}} = 4{S_{ACD}}\)
+) Chứng minh hai tam giác APQ và ACD đồng dạng. Sử dụng định lí : Tỉ số diện tích tam giác bằng bình phương tỉ số đồng dạng và công thức tính diện tích tam giác bằng nửa tích một cạnh và đường cao tương ứng, chứng minh \(AE = \dfrac{1}{2}AB \Rightarrow E \equiv O\).
+) Kết luận vị trí của đường kính CD so với AB.

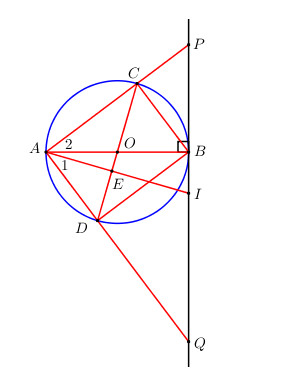
a) Ta có : \(\widehat {ACB} = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow AC \bot BC\).
\( \Rightarrow BC \bot AP\)
Xét tam giác vuông BCP có : \(\widehat {BPC} + \widehat {CBP} = {90^0}\)(tổng hai góc nhọn trong tam giác vuông)
Mà \(\widehat {ABC} + \widehat {CBP} = \widehat {ABP} = {90^0}\)
Advertisements (Quảng cáo)
\( \Rightarrow \widehat {ABC} = \widehat {BPC}\). Lại có \(\widehat {ABC} = \widehat {ADC}\) (hai góc nội tiếp cùng chắn cung AD)
\( \Rightarrow \widehat {ADC} = \widehat {BPC}\).
Ta có : \(\widehat {ADC} + \widehat {CDQ} = {180^0}\) (hai góc kề bù) \( \Rightarrow \widehat {BPC} + \widehat {CDQ} = {180^0}\).
Vậy tứ giác CPQD là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800).
b) Gọi \(E = AI \cap CD\).
Ta có : \(\widehat {CAD} = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow \Delta APQ\) vuông tại A \( \Rightarrow AI = \dfrac{1}{2}PQ = IP = IQ\) (định lí đường trung tuyến trong tam giác vuông).
\( \Rightarrow \Delta IAQ\) cân tại I \( \Rightarrow \widehat {{A_1}} = \widehat Q\) (2 góc ở đáy) (1)
Xét tam giác vuông APQ có: \(\widehat Q + \widehat P = {90^0}\) (tổng hai góc nhọn trong tam giác vuông)
Xét tam giác vuông ABP có: \(\widehat {{A_2}} + \widehat P = {90^0}\) (tổng hai góc nhọn trong tam giác vuông)
\( \Rightarrow \widehat {{A_2}} = \widehat Q\) (2). Từ (1) và (2) \( \Rightarrow \widehat {{A_1}} = \widehat {{A_2}}\).
Và \(\widehat {ADC} = \widehat {BPC}\,\,\,\left( {cmt} \right) \Rightarrow \Delta ADE\) có : \(\widehat {{A_1}} + \widehat {ADC} = \widehat {{A_2}} + \widehat {BPC} = {90^0} \Rightarrow \Delta ADE\) vuông tại E.
Vậy \(AI \bot CD\) tại E.
c) \({S_{CPQD}} = 3{S_{ACD}} \Rightarrow {S_{APQ}} = 4{S_{ACD}}\).
Xét \(\Delta APQ\) và \(\Delta ADC\) có : \(\widehat {PAQ}\) chung ; \(\widehat {BPC} = \widehat {ADC}\,\,\left( {cmt} \right)\)
\( \Rightarrow \Delta APQ \sim \Delta ADC\,\,\left( {g.g} \right) \Rightarrow \dfrac{{{S_{ACD}}}}{{{S_{APQ}}}} = {\left( {\dfrac{{CD}}{{PQ}}} \right)^2} = \dfrac{1}{4} \Leftrightarrow \dfrac{{CD}}{{PQ}} = \dfrac{1}{2}\)
Ta có : \(\dfrac{{{S_{ACD}}}}{{{S_{APQ}}}} = \dfrac{{\dfrac{1}{2}AE.CD}}{{\dfrac{1}{2}AB.PQ}} = \dfrac{{AE}}{{AB}}.\dfrac{{CD}}{{PQ}} \Rightarrow \dfrac{1}{4} = \dfrac{{AE}}{{AB}}.\dfrac{1}{2} \Rightarrow \dfrac{{AE}}{{AB}} = \dfrac{1}{2} \Rightarrow AE = \dfrac{1}{2}AB \Rightarrow E \equiv O\)
Mà \(AE \bot CD\,\,\left( {cmt} \right) \Rightarrow AO \bot CD\) hay \(AB \bot CD\).
Vậy khi \(CD \bot AB\) thì \({S_{CPQD}} = 3{S_{ACD}}.\)
