
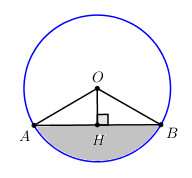
Hình viên phân AB trong hình tròn (O ; R) là phần hình tròn giới hạn bởi cung nhỏ AB và dây AB. Hãy tính diện tích hình viên phân AB biết \(\widehat {AOB} = {120^o}\) và R = 10 cm.
Diện tích hình viên phân AB bằng diện tích hình quạt OAB trừ diện tích tam giác OAB.

Advertisements (Quảng cáo)
Gọi H là trung điểm của AB \( \Rightarrow OH \bot AB\) (quan hệ vuông góc giữa đường kính và dây cung).
Xét tam giác OAB có \(OA = OB = R \Rightarrow \Delta OAB\) cân tại O \( \Rightarrow \) Đường cao OH đồng thời là phân giác \( \Rightarrow \widehat {AOH} = \widehat {BOH} = \dfrac{1}{2}\widehat {AOB} = \dfrac{1}{2}{.120^0} = {60^0}\).
Xét tam giác vuông OAH có:
\(\begin{array}{l}OH = OA.\cos {60^0} = 10.\dfrac{1}{2} = 5\,\,\left( {cm} \right)\\AH = OA.\sin {60^0} = 10.\dfrac{{\sqrt 3 }}{2} = 5\sqrt 3 \,\,\left( {cm} \right)\\ \Rightarrow AB = 2AH = 10\sqrt 3 \left( {cm} \right)\end{array}\)
\( \Rightarrow {S_{\Delta OAB}} = \dfrac{1}{2}OH.AB = \dfrac{1}{2}.5.10\sqrt 3 = 25\sqrt 3 \,\,\left( {c{m^2}} \right)\).
Diện tích hình quạt OAB là \({S_q} = \dfrac{{\pi .{R^2}n}}{{360}} = \dfrac{{\pi {{.10}^2}.120}}{{360}} = \dfrac{{100\pi }}{3}\,\,\left( {c{m^2}} \right)\).
Vậy diện tích hình viên phân AB là: \(S = {S_q} - {S_{\Delta OAB}} = \dfrac{{100\pi }}{3} - 25\sqrt 3 \,\,\left( {c{m^2}} \right)\).
Baitapsgk.com
