Advertisements (Quảng cáo)
Cho điểm C nằm bên trong đoạn thẳng AB. Vẽ các nửa đường tròn đường kính AB, AC, CB ở về cùng phía với AB. Vẽ đường thẳng vuông góc với AB tại C cắt nửa đường tròn đường kính AB tại D. Chứng minh diện tích giới hạn bởi ba nửa đường tròn nói trên bằng diện tích hình tròn đường kính CD.
+) Sử dụng công thức tính diện tích hình tròn \(S = \pi {R^2}\).
+) Áp dụng hằng đẳng thức và hệ thức lượng trong tam giác vuông chứng minh 2 phần diện tích đó bằng nhau.
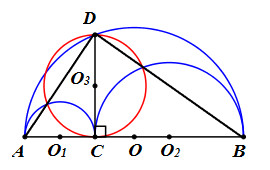
Gọi O, O1, O2, O3 lần lượt là tâm các đường tròn đường kính AB, AC, BC, CD.
Diện tích giới hạn bởi ba đường tròn đường kính AB, AC, CB là:
Advertisements (Quảng cáo)
\(\begin{array}{l}{S_1} = \dfrac{1}{2}\pi .{\left( {\dfrac{{AB}}{2}} \right)^2} – \dfrac{1}{2}\pi .{\left( {\dfrac{{AC}}{2}} \right)^2} – \dfrac{1}{2}\pi {\left( {\dfrac{{BC}}{2}} \right)^2}\\\,\,\,\,\, = \dfrac{1}{8}\pi \left( {A{B^2} – A{C^2} – B{C^2}} \right)\end{array}\)
Ta có: \(AB = AC + BC\) \( \Rightarrow A{B^2} = {\left( {AC + BC} \right)^2} = A{C^2} + B{C^2} + 2AC.BC\)
\( \Rightarrow {S_1} = \dfrac{1}{8}\pi \left( {A{C^2} + B{C^2} + 2AC.BC – A{C^2} – B{C^2}} \right) \)\(\,= \dfrac{1}{4}\pi .AC.BC\)
Diện tích hình tròn đường kính \(CD\) là \({S_2} = \pi {\left( {\dfrac{{CD}}{2}} \right)^2} = \dfrac{1}{4}\pi C{D^2}\) .
Ta có: \(\widehat {ADB}\) nội tiếp chắn nửa đường tròn đường kính AB \( \Rightarrow \widehat {ADB} = {90^0} \Rightarrow \Delta ABD\) vuông tại D.
Áp dụng hệ thức lượng trong tam giác vuông ABD có: \(C{D^2} = AC.BC\)
\( \Rightarrow {S_2} = \dfrac{1}{4}\pi .AC.BC = {S_1}\,\,\left( {dpcm} \right)\).
Baitapsgk.com