
Hãy tính thể tích các hình khối dưới đây theo kích thước đã cho.
Sử dụng công thức tính thể tích khối cầu \(V = \dfrac{4}{3}\pi {R^3}\), thể tích khối trụ \(V = \pi {R^2}h\), thể tích khối nón \(V = \dfrac{1}{3}\pi {R^2}h\), thể tích khối nón cụt \(V = \dfrac{1}{3}\pi h\left( {r_1^2 + {r_1}{r_2} + r_2^2} \right)\).

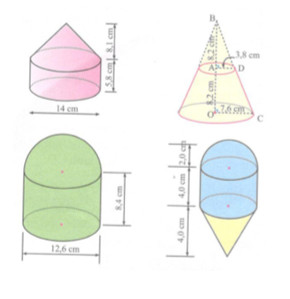
Hình 1: Bao gồm 1 hình nón và 1 hình trụ.
Advertisements (Quảng cáo)
\({V_1} = {V_\text{nón}} + {V_\text{trụ}} = \dfrac{1}{3}\pi {.7^2}.8,1 + \pi {.7^2}.5,8 \)\(\,= \dfrac{{833\pi }}{2}\,\,\left( {c{m^3}} \right)\).
Hình 2: Là 1 hình nón cụt.
\({V_2} = \dfrac{1}{3}\pi \left( {3,{8^2} + 3,8.7,6 + 7,{6^2}} \right).8,2 \)\(\,\approx 14448\,\,\left( {c{m^3}} \right)\).
Hình 3: Bao gồm 1 hình bán cầu và 1 hình trụ.
\({V_3} = \dfrac{1}{2}{V_\text{cầu}} + {V_\text{trụ}}\)\(\, = \dfrac{1}{2}.\dfrac{4}{3}\pi .6,{3^3} + \pi .6,{3^2}.8,4 \)\(\,\approx 1517,1\,\,\left( {c{m^3}} \right)\).
Hình 4: Bao gồm 1 hình bán cầu, 1 hình trụ và 1 hình nón.
\({V_4} = \dfrac{1}{2}{V_\text{cầu}} + {V_\text{trụ}} + {V_\text{nón}}\)\(\, = \dfrac{1}{2}.\dfrac{4}{3}\pi {.2^3} + \pi {.2^2}.4 + \dfrac{1}{3}\pi {.2^2}.4\)\(\, = \dfrac{{80\pi }}{3}\,\,\left( {c{m^3}} \right)\).
Baitapsgk.com
