
Hãy tính thể tích, diện tích bề mặt một chi tiết máy theo kích thước đã cho trong hình sau:
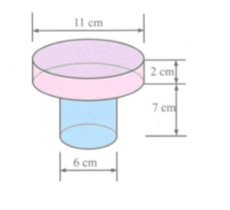
Chi tiết máy đã cho được tạo nên bởi 2 hình trụ, áp dụng các công thức tính diện tích xung quanh, diện tích toàn phần và thể tích của khối trụ.

Chi tiết máy được tạp nên bởi 2 hình trụ.
Hình trụ thứ nhất có bán kính đáy \({R_1} = 5,5cm\), chiều cao \({h_1} = 2cm\)
\( \Rightarrow \) Diện tích toàn phần của hình trụ thứ nhất là
Advertisements (Quảng cáo)
\({S_{tp1}} = 2\pi {R_1}{h_1} + 2\pi R_1^2 \)\(\,= 2\pi .5,5.2 + 2\pi {.2^2} = 30\pi \,\,\left( {c{m^2}} \right)\)
Thể tích của hình trụ thứ nhất là \({V_1} = \pi R_1^2{h_1} = \pi .5,{5^2}.2 = \dfrac{{121\pi }}{2}\,\,\left( {c{m^3}} \right)\).
Hình trụ thứ nhất có bán kính đáy \({R_2} = 3cm\), chiều cao \({h_1} = 7cm\)
\( \Rightarrow \) Diện tích toàn phần của hình trụ thứ nhất là
\({S_{tp2}} = 2\pi {R_2}{h_2} + 2\pi R_2^2\)\(\, = 2\pi .3.7 + 2\pi {.3^2} = 60\pi \,\,\left( {c{m^2}} \right)\)
Thể tích của hình trụ thứ nhất là \({V_2} = \pi R_2^2{h_2} = \pi {.3^2}.7 = 63\pi \,\,\left( {c{m^3}} \right)\).
Do phần diện tích tiếp xúc giữa 2 hình trụ được tính 2 lần nên diện tích bề mặt của chi tiết máy là
\(S = {S_{tp1}} + {S_{tp2}} - {S_{tx}} \)\(\,= 30\pi + 60\pi - \pi {.3^2} = 81\pi \,\,\left( {c{m^2}} \right)\).
Thể tích của chi tiết máy là \(V = {V_1} + {V_2} = \dfrac{{121}}{2}\pi + 63\pi = \dfrac{{247}}{2}\pi \,\,\left( {c{m^3}} \right)\).
Baitapsgk.com
