Bài tập - Chủ đề 3: Tứ giác nội tiếp - Bài 3 trang 102 Tài liệu dạy – học Toán 9 tập 2. Giải bài tập Từ một điểm M nằm ngoài đường tròn (O) vẽ cát tuyến MBC và tiếp tuyến Mt tiếp xúc với (O)
Từ một điểm M nằm ngoài đường tròn (O) vẽ cát tuyến MBC và tiếp tuyến Mt tiếp xúc với (O) tại A. Gọi I là trung điểm của dây BC. Chứng minh AMIO là một tứ giác nội tiếp.
Tứ giác có tổng hai góc đối bằng 1800 là tứ giác nội tiếp.
Advertisements (Quảng cáo)
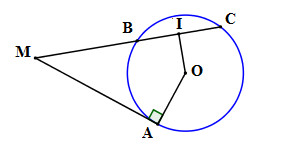
I là trung điểm của BC \( \Rightarrow OI \bot BC\) (quan hệ vuông góc giữa đường kính và dây cung)
\( \Rightarrow \widehat {OIM} = {90^0}\)
Xét tứ giác AMIO có: \(\widehat {OIM} + \widehat {OAM} = {90^0} + {90^0} = {180^0} \Rightarrow \) Tứ giác AMIO là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800).