
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài với nhau tại điểm A. Hai dây cung BA và CA của (O) kéo dài cắt (O’) lần lượt tại D và E. Chứng minh \(\widehat {ABC} = \widehat {ADE}\).
+) Dựng tiếp tuyến chung của hai đường tròn \(\left( O \right)\) và \(\left( {O’} \right)\) tại A.
+) Sử dụng tính chất: Trong một đường tròn, góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn 1 cung thì bằng nhau.

Advertisements (Quảng cáo)
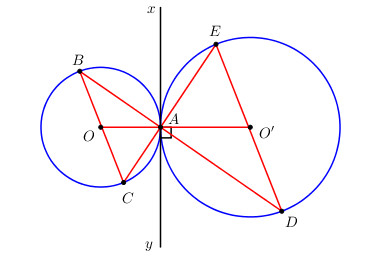
Qua A kẻ đường thẳng \(xy \bot OO’\), khi đó xy là tiếp tuyến chung của 2 đường tròn \(\left( O \right)\) và \(\left( {O’} \right)\) tại A.
Xét đường tròn \(\left( O \right)\) ta có: \(\widehat {ABC} = \widehat {CAy}\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cing cùng chắn cung AC).
Xét đường tròn \(\left( {O’} \right)\) ta có: \(\widehat {ADE} = \widehat {EAx}\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cing cùng chắn cung AE).
Mà \(\widehat {CAy} = \widehat {EAx}\) (hai góc đối đỉnh).
Vậy \(\widehat {ABC} = \widehat {ADE}\) (đpcm).
